Orientuotieji grafai, Topologinis rikiavimas¶
It is amazing how often messy applied problems have a simple descriptionand solution in terms of classical graph properties.Nuostabu, kaip dažnai sudėtingus praktinius uždavinius pavykstapaprastai suformuluoti ir išspręsti naudojant grafų teoriją.Stivenas S. Skiena (Steven S. Skienna)
Iki šiol nagrinėjome tik paprasčiausius grafus: juose briaunos rodo, kad tarp dviejų objektų ryšys yra arba jo nėra. Tačiau ne visada ryšys tarp objektų esti vienodas. Šiame ir tolesniame skyreliuose praplėsime grafo sąvoką ir panagrinėsime uždavinius, modeliuojamus sudėtingesniais grafais.
Orientuotieji grafai¶
Kartais gali tekti grafais pavaizduoti nesimetrišką ryšį tarp
objektų. Pavyzdžiui, jei grafu norėtume vaizduoti miesto planą, kur
viršūnės atitiktų sankryžas, o briaunos – jas jungiančias
gatves, tai galbūt tektų parodyti, kad kai kurios gatvės yra vienos
krypties eismo: iš sankryžos 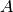 galima nuvažiuoti į
sankryžą
galima nuvažiuoti į
sankryžą 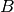 , bet ne atvirkščiai. Tarkime, atėjo pavasaris ir
grafu modeliuojame, kuri mergaitė patinka kuriam berniukui, ir kuriai
mergaitei – kuris berniukas. Čia vėl (deja!) susiduriame su
nesimetrišku sąryšiu: Pauliui gali patikti Milda, o ši galbūt net
nežvilgtelės į jo pusę.
, bet ne atvirkščiai. Tarkime, atėjo pavasaris ir
grafu modeliuojame, kuri mergaitė patinka kuriam berniukui, ir kuriai
mergaitei – kuris berniukas. Čia vėl (deja!) susiduriame su
nesimetrišku sąryšiu: Pauliui gali patikti Milda, o ši galbūt net
nežvilgtelės į jo pusę.
Taigi kartais prasminga grafo briaunoms suteikti kryptį. Grafas,
kuriame briaunos turi kryptį, vadinamas orientuotu arba
kryptiniu, o tokio grafo briaunos (su kryptimi) vadinamos
lankais. Piešiant grafą, lankai vaizduojami rodyklėmis. Jei
lankas nukreiptas iš viršūnės 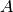 į viršūnę
į viršūnę 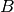 ,
sakoma, kad lankas išeina iš viršūnės
,
sakoma, kad lankas išeina iš viršūnės 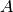 ir ateina į
viršūnę
ir ateina į
viršūnę 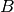 .
.
Ankstesniame skyrelyje buvome apibrėžę kai kurias grafų teorijos sąvokas, kurias reikėtų patikslinti orientuotiems grafams: viršūnės laipsnis, kelias, jungus grafas.
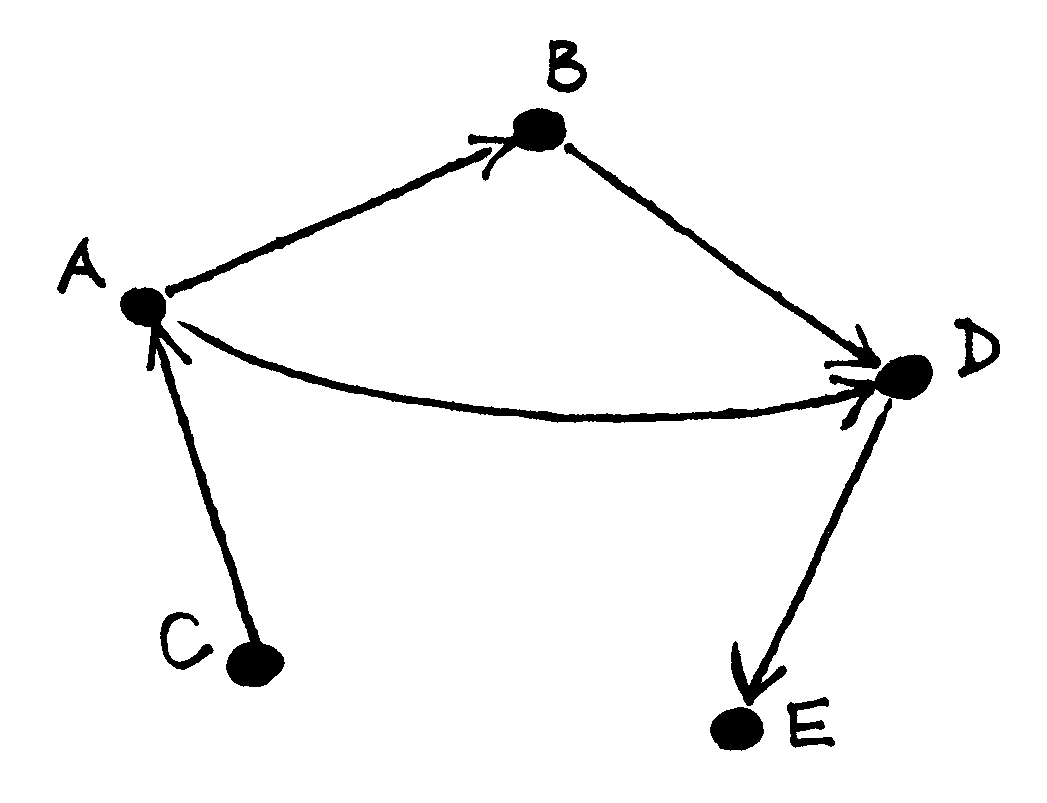
Fig. 52 Orientuotojo grafo pavyzdys¶
Orientuoto grafo viršūnės išėjimo laipsnis lygus lankų, išeinančių iš šios viršūnės, skaičiui, o įėjimo laipsnis lygus įeinančių į viršūnę lankų skaičiui.
Kelias ir ciklas orientuotame grafe traktuojamas taip pat, kaip ir neorientuotame grafe, tačiau einama tik lanko kryptimi.
Orientuotame grafe yra keli jungumo tipai. Orientuotas grafas vadinamas silpnai jungiu, jei orientuotą grafą pakeitus jį atitinkančiu neorientuotu grafu (t. y. grafo lankus pakeitus briaunomis), šis yra jungus.
Vienkryptiškai jungiu grafu vadinamas orientuotas grafas, jei
pasirinkus bet kurias dvi viršūnes 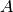 ir
ir 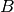 , egzistuoja
kelias iš
, egzistuoja
kelias iš 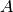 į
į 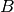 arba iš
arba iš 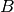 į
į 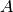 .
.
Orientuotas grafas yra stipriai jungus (stipriai susietas), jei iš bet kurios viršūnės galima pasiekti bet kurią kitą viršūnę.
Visi stipriai jungūs grafai yra ir vienkryptiškai jungūs, o visi vienkryptiškai jungūs yra ir silpnai jungūs.
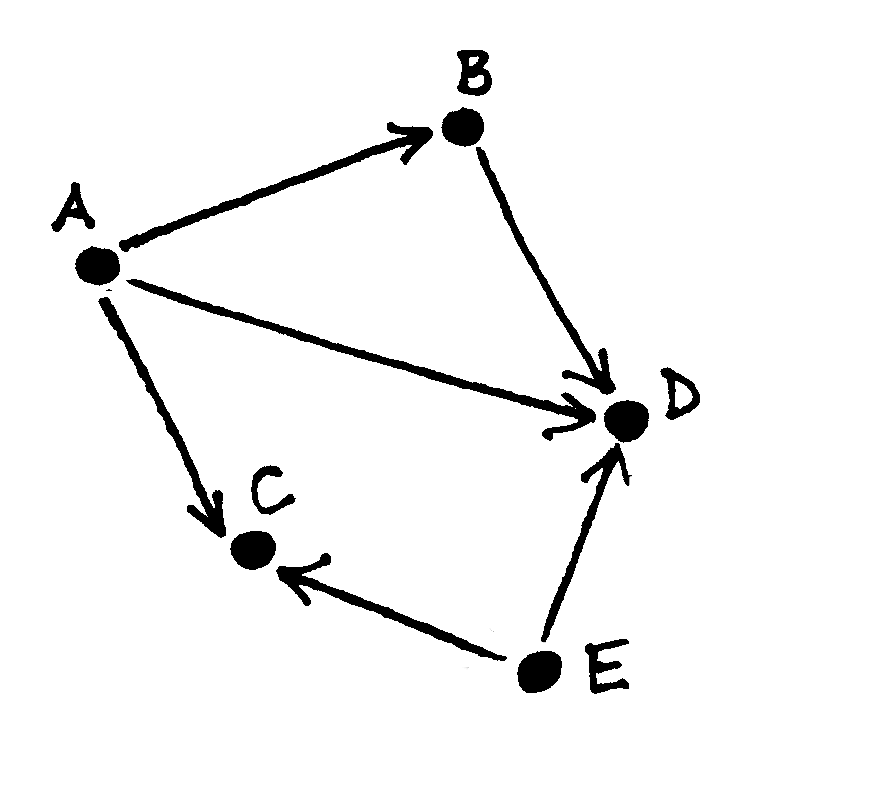
Fig. 53 Silpnai jungus grafas¶
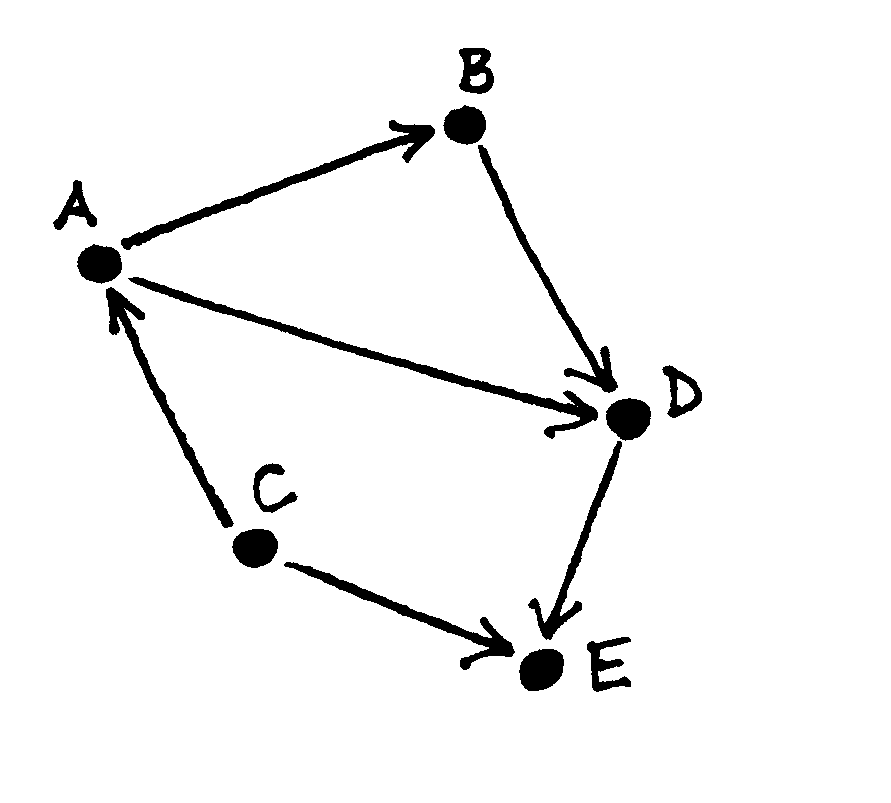
Fig. 54 Vienkryptiškai jungus grafas¶
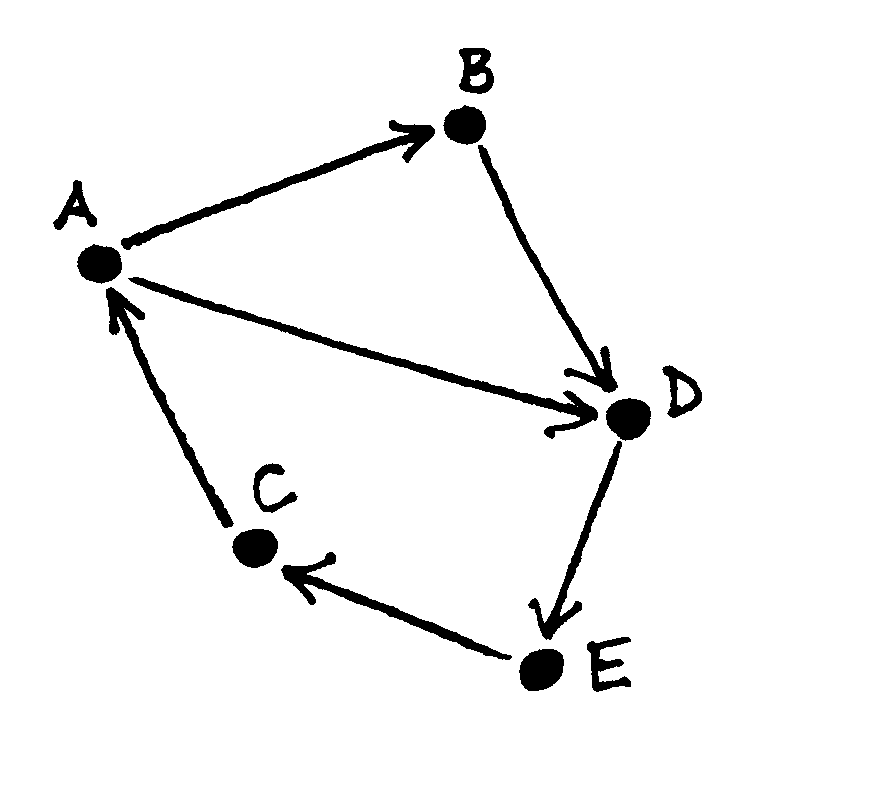
Fig. 55 Stipriai jungus grafas¶
Orientuotas grafas yra bendresnis grafo atvejis, ir atvirkščiai –
paprastas grafas 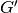 yra atskiras orientuoto grafo
yra atskiras orientuoto grafo 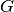 atvejis, kuriame grafo
atvejis, kuriame grafo 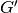 briauną
briauną 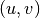 atitinka du
lankai
atitinka du
lankai 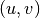 ir
ir 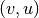 . Taigi nereikia beveik jokių
pakeitimų norint pavaizduoti orientuotą grafą kompiuteriu. Jei grafą
vaizduojame kaimynystės matrica, tai ši matrica tiesiog nebus
simetrinė (lanko įterpimas į grafą reikš reikšmės įrašymą į
vieną matricos langelį). Jei grafą vaizduojame kaimynystės
sąrašais, tai lanko įterpimas į grafą reikš vienos viršūnės
kaimynių sąrašo papildymą (dar mažiau darbo negu vaizduojant
paprastą grafą).
. Taigi nereikia beveik jokių
pakeitimų norint pavaizduoti orientuotą grafą kompiuteriu. Jei grafą
vaizduojame kaimynystės matrica, tai ši matrica tiesiog nebus
simetrinė (lanko įterpimas į grafą reikš reikšmės įrašymą į
vieną matricos langelį). Jei grafą vaizduojame kaimynystės
sąrašais, tai lanko įterpimas į grafą reikš vienos viršūnės
kaimynių sąrašo papildymą (dar mažiau darbo negu vaizduojant
paprastą grafą).
Beveik be jokių pakeitimų orientuotuose grafuose veiks jau aptarti algoritmai: paieška gilyn ir platyn, Oilerio ciklų bei Hamiltono ciklų paieška. Tiesa, algoritmai turės naują prasmę. Pavyzdžiui, paieškos gilyn ir platyn algoritmai aplankys ne visas vizualiai prijungtas viršūnes, bet tik tas, kurios pasiekiamos einant lankais (tik viena briaunos kryptimi). Šiek tiek skiriasi Oilerio ciklo egzistavimo sąlyga, tačiau ji labai natūrali: įeinančių lankų skaičius (įėjimo laipsnis) turi būti lygus išeinančių lankų skaičiui (išėjimo laipsniui) kiekvienoje viršūnėje (į kiekvieną viršūnę turime ateiti tiek kartų, kiek ir išeiti).
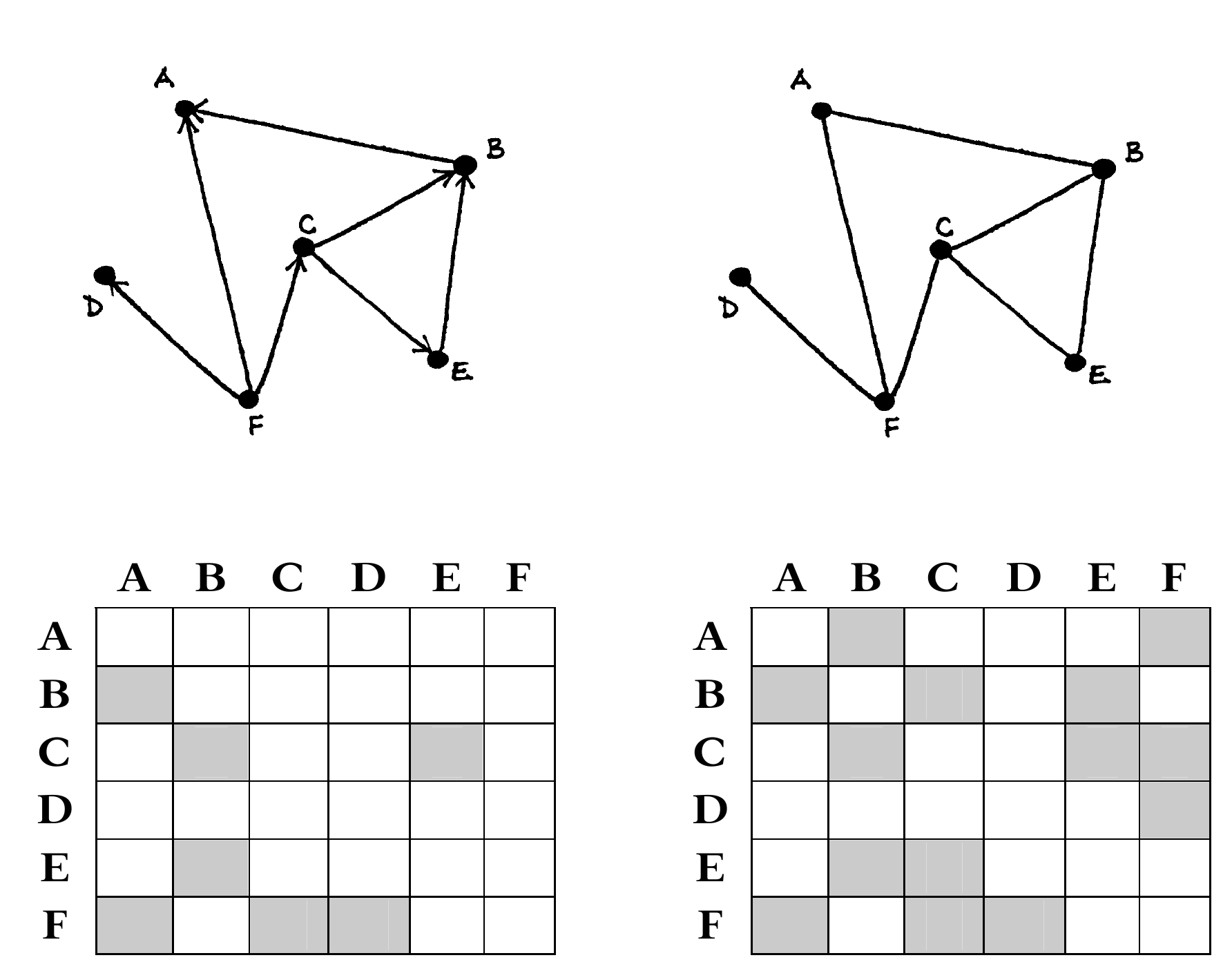
Fig. 56 Paveiksle pavaizduotas orientuotas grafas, jį atitinkantis neorientuotas grafas bei šiuos grafus atitinkanti kaimynystės matrica; matome, kad vienu atveju matrica yra simetriška, kitu atveju – ne¶
Topologinis rikiavimas¶
Įsivaizduokite, kad pradėjote ruoštis atostogoms ir norite keliauti
į tolimą šalį. Teks nuveikti nemažai darbų: užsisakyti lėktuvo
bilietus, numatyti ar užsisakyti nakvynės vietas, susipakuoti daiktus,
galbūt gauti vizas, išsirinkti valstybę, į kurią vyksite,
susiplanuoti maršrutą ir t. t. Akivaizdu, kad šių darbų bet kokia
tvarka atlikti negalima. Prieš perkant lėktuvo bilietus būtina
išsirinkti valstybę, į kurią vyksite, prieš numatant nakvynės
vietas – susiplanuoti maršrutą, kuriuo keliausite. Reikia visus
pasiruošimo atostogoms darbus surikiuoti į eilę taip, kad juos
atlikdami ta tvarka sėkmingai išvyktume atostogauti. Darbus galime
vaizduoti grafo viršūnėmis, o faktą, kad darbas 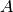 turi būti
atliktas prieš darbą
turi būti
atliktas prieš darbą 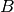 , žymėti lanku iš
, žymėti lanku iš 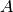 į
į
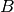 .
.
Šis uždavinys bus grafo topologinio rikiavimo uždavinys:
orientuoto grafo viršūnes reikia išrikiuoti į vieną eilę taip, kad
bet kuriam grafo lankui 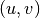 , toje eilėje viršūnė
, toje eilėje viršūnė
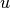 eitų prieš viršūnę
eitų prieš viršūnę  .
.
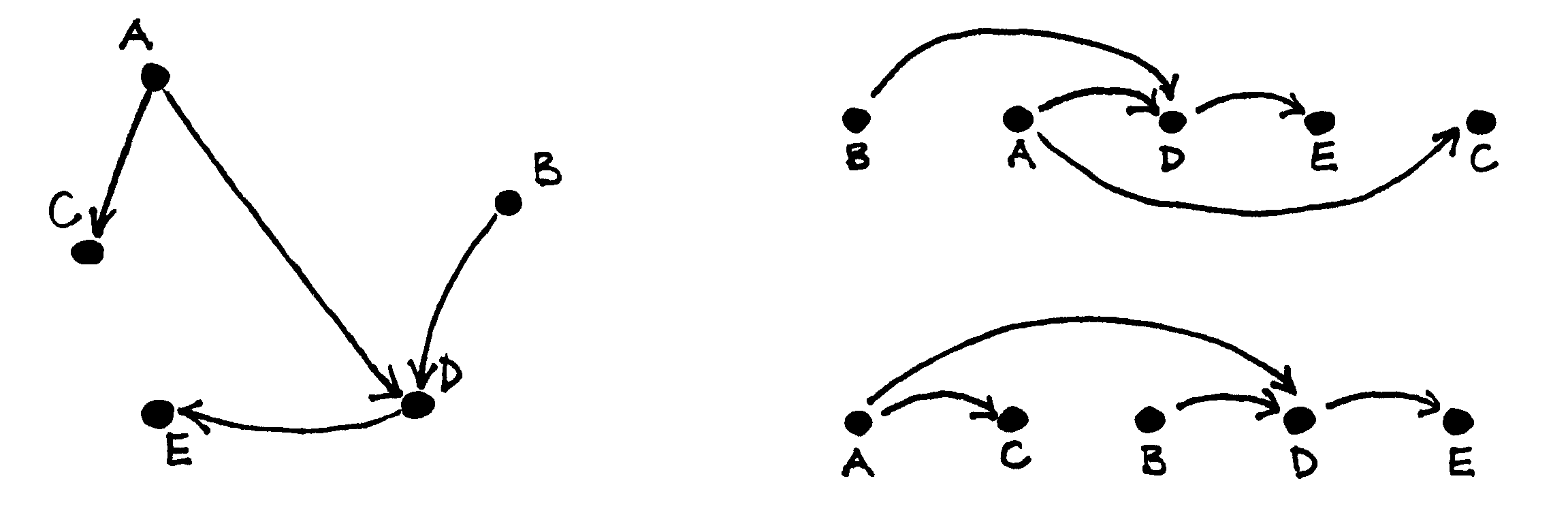
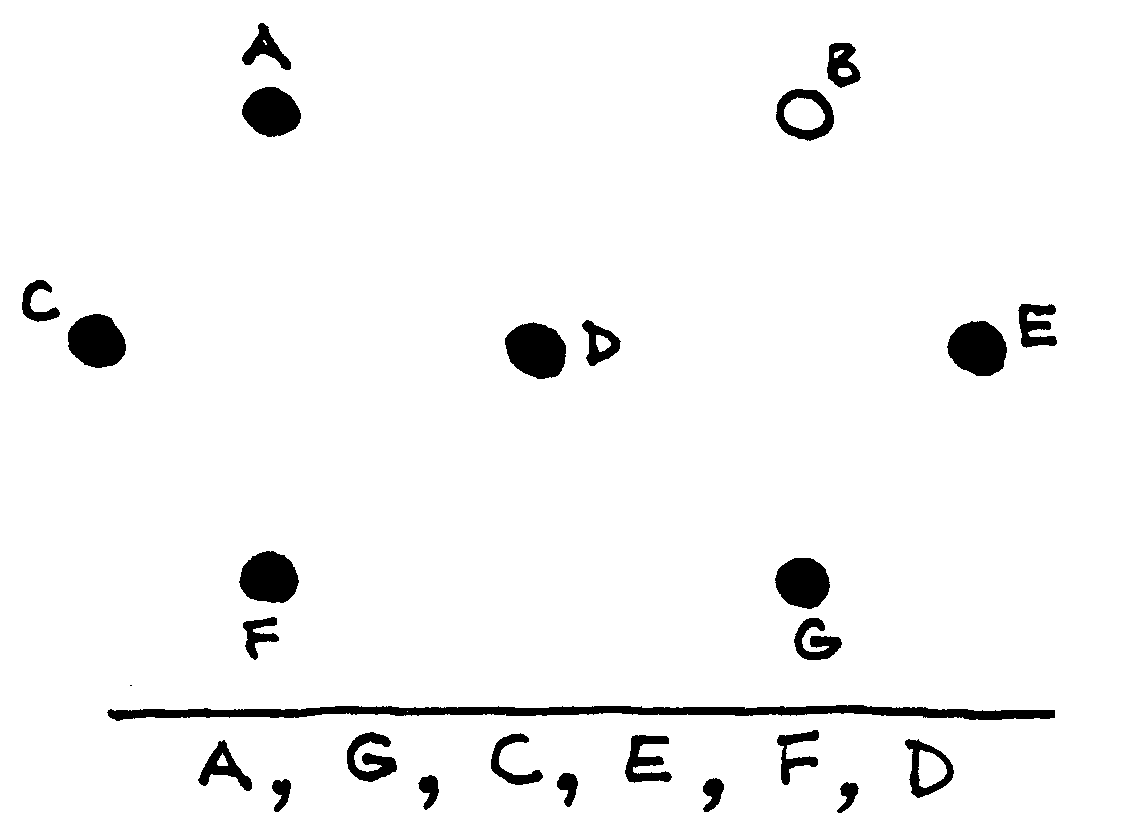
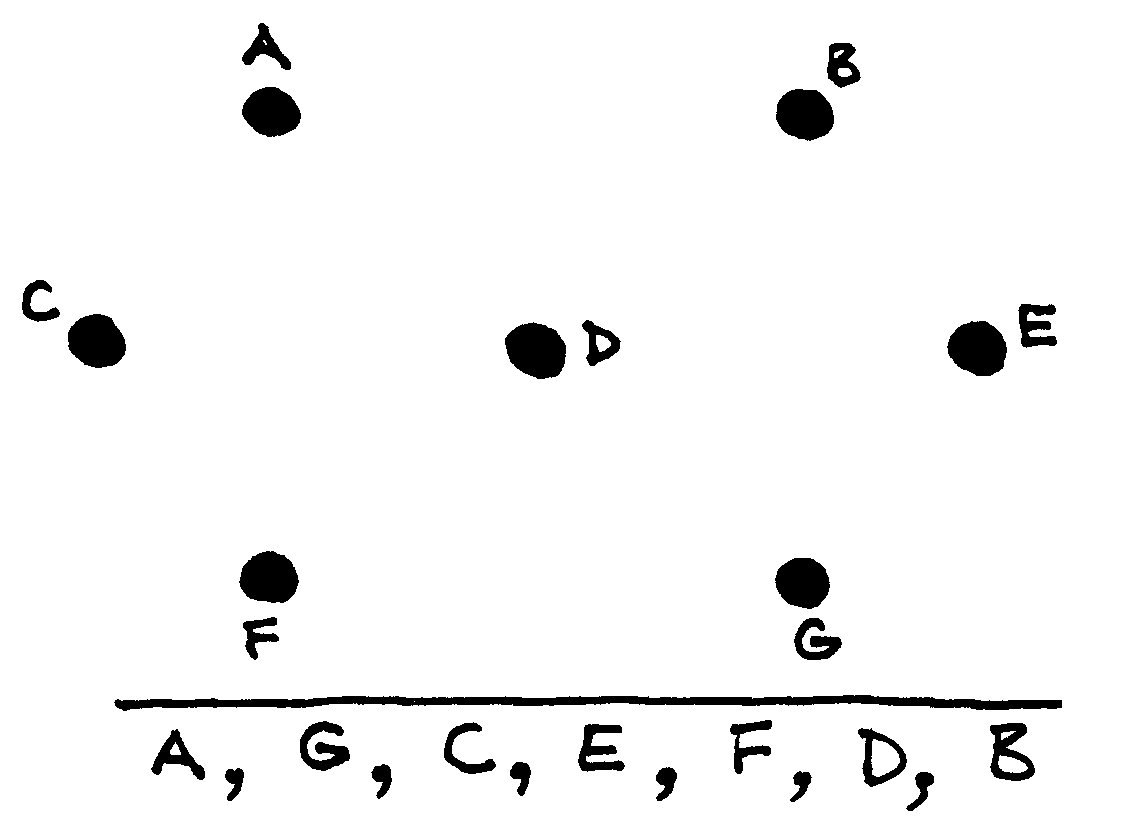
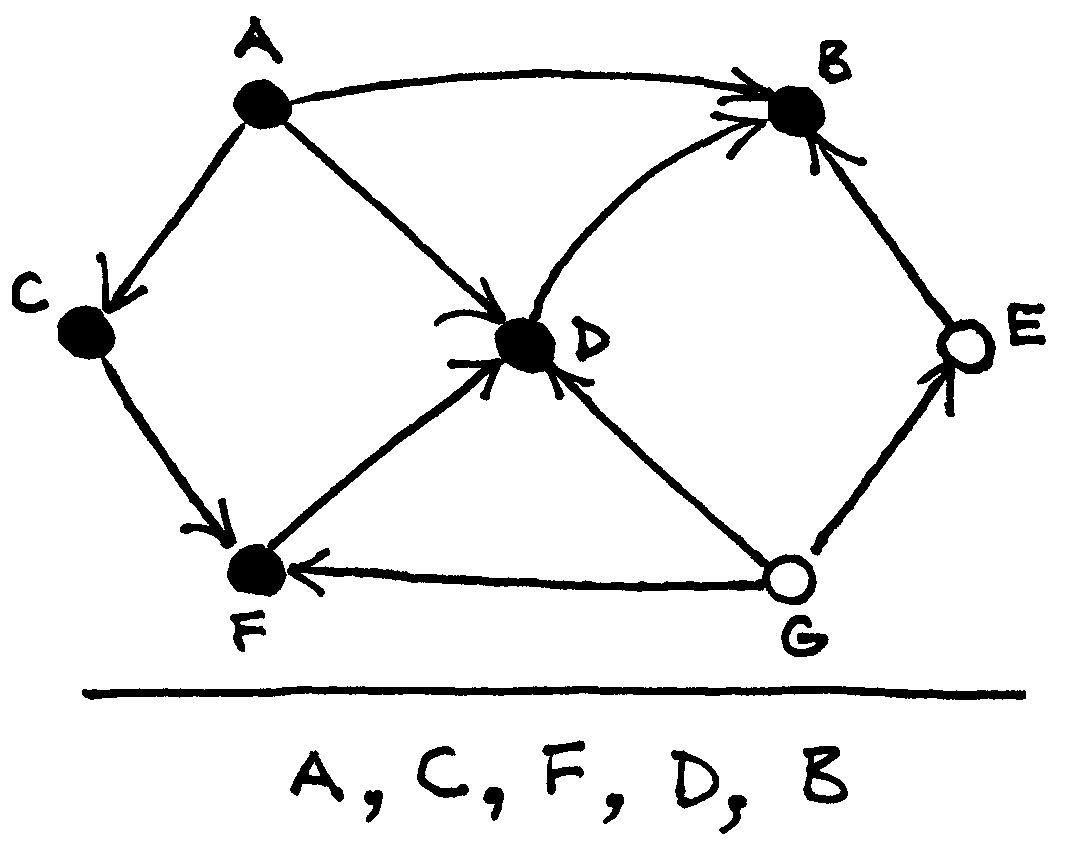
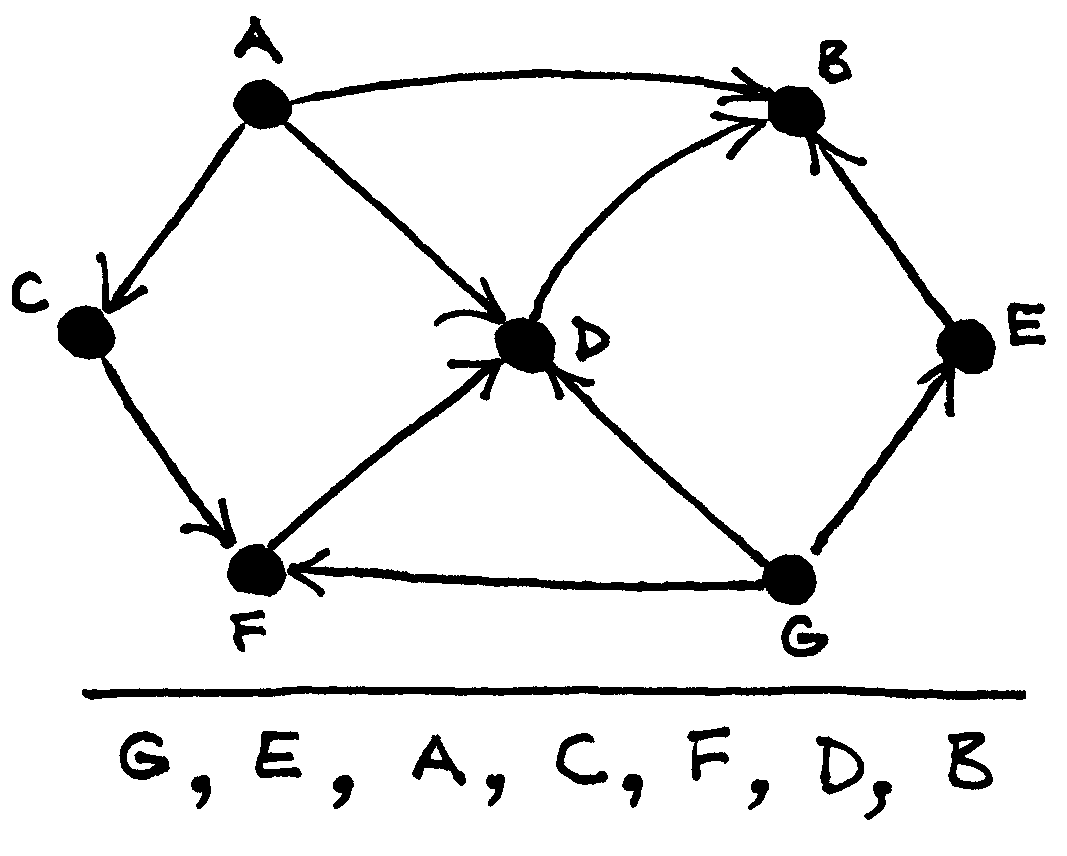
Fig. 57 Orientuotas beciklis grafas ir du skirtingi topologiniai jo išrikiavimai¶
Ar visada galima topologiškai surikiuoti grafo viršūnes? Tarkime, kad
darbas 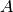 turi būti atliktas prieš darbą
turi būti atliktas prieš darbą 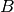 , darbas
, darbas
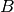 – prieš darbą
– prieš darbą 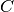 , o darbas
, o darbas 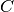 – prieš
darbą
– prieš
darbą 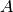 . Topologiškai surikiuoti tokios darbų sekos
neįmanoma, tačiau ir pačios darbų sekos turbūt negalima pavadinti
korektiška. Tad grafo viršūnes topologiškai galima išrikiuoti, jei
ir tik jei grafe nėra ciklų.
. Topologiškai surikiuoti tokios darbų sekos
neįmanoma, tačiau ir pačios darbų sekos turbūt negalima pavadinti
korektiška. Tad grafo viršūnes topologiškai galima išrikiuoti, jei
ir tik jei grafe nėra ciklų.
Topologinio rikiavimo algoritmas gana intuityvus: pirma išrenkamos ir į seką įtraukiamos viršūnės, kurių įėjimo laipsniai lygūs 0 (iš tiesų reikia pradėti nuo darbų, prieš kuriuos nieko daugiau nereikia atlikti). Tuomet pašalinami iš šių viršūnių išeinantys lankai ir atnaujinama informacija apie visų viršūnių laipsnius. Toliau vėl kartojami tie patys veiksmai, kol į seką įtraukiamos visos viršūnės.
Orientuotas beciklis grafas;
viršūnių |
Pašalinami lankai, išeinantys iš
viršūnių |
Į seką įtraukiamos naujos
viršūnės |
Pašalinamas lankas, išeinantis iš
viršūnės |
Norint efektyviai vykdyti algoritmo žingsnius, grafą reikia vaizduoti kaimynystės sąrašais. Viršūnių, kurios neturi įeinančių lankų, galima ieškoti kiekvienąkart ciklu perbėgant visas viršūnes. Tačiau efektyviau laikyti eilę viršūnių, kurių įėjimo laipsniai lygūs 0, ir ją vis papildyti iš grafo trinant lankus. Tam panaudosime eilės duomenų struktūrą, aprašytą Paieška platyn skyrelyje.
const MAXN = ...; { maksimalus viršūnių skaičius }
MAXB = MAXN*MAXN; { maksimalus lankų skaičius }
type viršūnė = record
k : integer; { kaimynių skaičius ir sąrašas }
ksąrašas : array [1..MAXN] of integer;
end;
grafas = record
n : integer; { viršūnių skaičius }
laipsnis : array [1..MAXN] of integer;
{ įėjimo laipsnis }
vir : array [1..MAXN] of viršūnė;
{ viršūnių sąrašas }
end;
procedure topologinis_rikiavimas(var g : grafas;
var seka : masyvas);
{ topologinis išrikiavimas įrašomas į masyvą seka }
var v, u, i, nr : integer;
eil : eilė;
begin
išvalyk(eil);
{ į eilę įtraukiamos viršūnės, kurių įėjimo laipsniai lygūs 0 }
for v := 1 to g.n do
if g.laipsnis[v] = 0 then
įdėk(eil, v);
nr := 0; { išrikiuotų viršūnių sekos indeksas }
while not tuščia(eil) do begin
v := išimk(eil);
nr := nr + 1;
seka[nr] := v; { v įrašoma į seką }
{ „ištrinami“ iš v išeinantys lankai ir papildoma eilė }
for i := 1 to g.vir[v].k do begin
u := g.vir[v].ksąrašas[i]; { kaimynė }
g.laipsnis[u] := g.laipsnis[u] - 1;
if g.laipsnis[u] = 0 then
įdėk(eil, u);
end;
end;
end;
const int MAXN = ...; // maksimalus viršūnių skaičius
int n; // viršūnių skaičius
vector<int> adj[MAXN]; // adj[i] yra i-tosios viršūnės kaimynų sąrašas
int laipsnis[MAXN]; // įėjimo laipsniai
vector<int> seka;
void toposort () {
// topologinis išrikiavimas bus įrašomas į vektorių "seka"
queue<int> q;
for (int i = 0; i < n; i++)
if (laipsnis[i] == 0)
q.push(i);
while (!q.empty()) {
int v = q.front();
q.pop();
seka.push_back(v); // v įrašomas į seką
// "ištrinami" iš v išeinantys lankai ir papildoma eilė
for (int u : adj[v]) {
// u - viršūnės v kaimynė
laipsnis[u]--;
if (laipsnis[u] == 0)
q.push(u);
}
}
}
Jei baigus vykdyti algoritmą, į seką nebuvo įtrauktos visos
viršūnės (t. y. nr < g.n), tai reiškia, kad grafe aptikta
ciklų, ir topologinis išrikiavimas neįmanomas. Atkreipkite dėmesį,
jog pateiktoje procedūroje grafo lankai iš tiesų nėra ištrinami,
tik atnaujinama informacija apie viršūnių įeinančius laipsnius.
Šio algoritmo sudėtingumas – 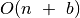 , kur
, kur 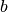 –
lankų skaičius.
–
lankų skaičius.
Yra ir kitas tokio paties sudėtingumo topologinio rikiavimo algoritmas, naudojantis paiešką gilyn; šį algoritmą realizuoti yra paprasčiau. Jo teksto nepateiksime, tik trumpai paaiškinsime idėją.
Pasirinkus bet kurią viršūnę, nuo jos atliekama paieška gilyn. Paieškos
gilyn metu pirmiausia juodai nuspalvinamos „giliausios“ viršūnės: jei
orientuotasis grafas neturi ciklų, tai viršūnė  bus
nuspalvinta juodai tik tada, kai jau nuspalvintos juodai visos iš jos
pasiekiamos viršūnės. Todėl jei spalvinant viršūnę juodai, ji dar
ir įterpiama į sekos pradžią, tai gautoji seka ir yra topologinis
grafo išrikiavimas.
bus
nuspalvinta juodai tik tada, kai jau nuspalvintos juodai visos iš jos
pasiekiamos viršūnės. Todėl jei spalvinant viršūnę juodai, ji dar
ir įterpiama į sekos pradžią, tai gautoji seka ir yra topologinis
grafo išrikiavimas.
Jei paieška gilyn baigta, bet dar likę baltų viršūnių, tuomet vėl pasirenkama bet kuri balta viršūnė ir nuo jos atliekama paieška gilyn, kartojant jau aprašytus veiksmus. Šis algoritmas taip pat gali aptikti ciklą grafe: nagrinėjant viršūnės kaimynes neturi būti aptinkama pilka viršūnė, nes joje pradėta ir dar nebaigta paieška gilyn.
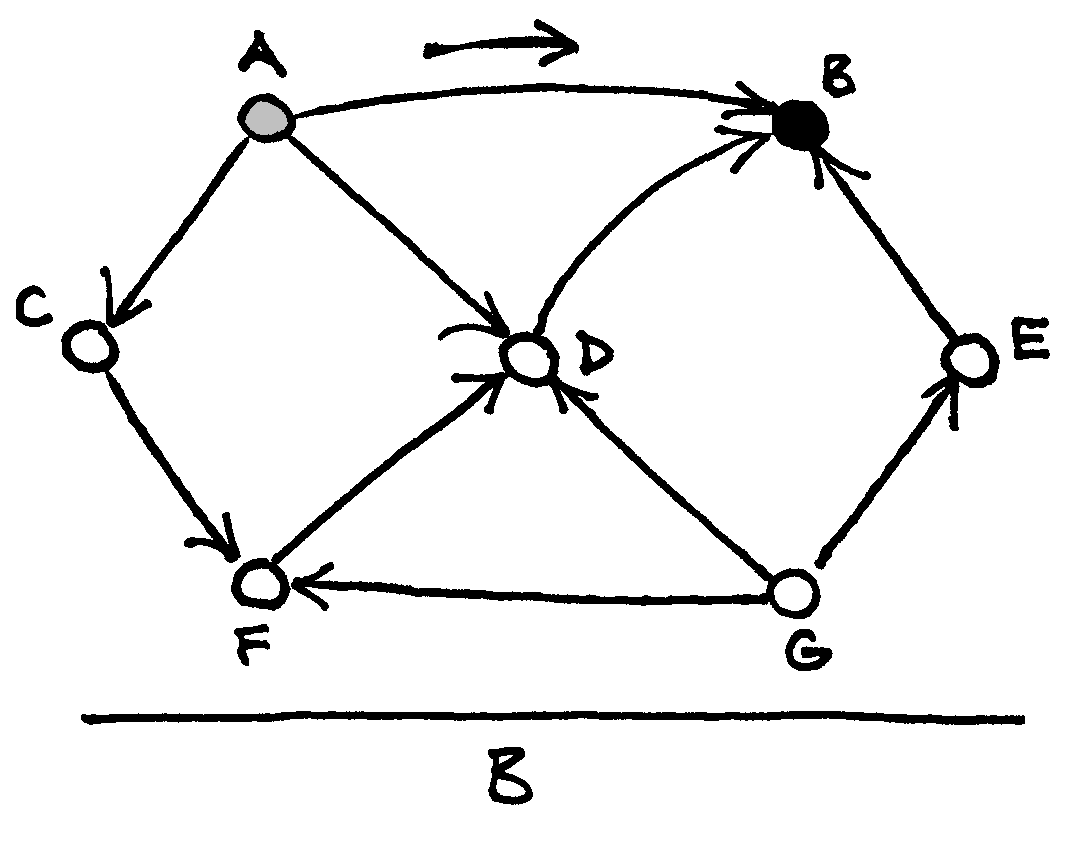
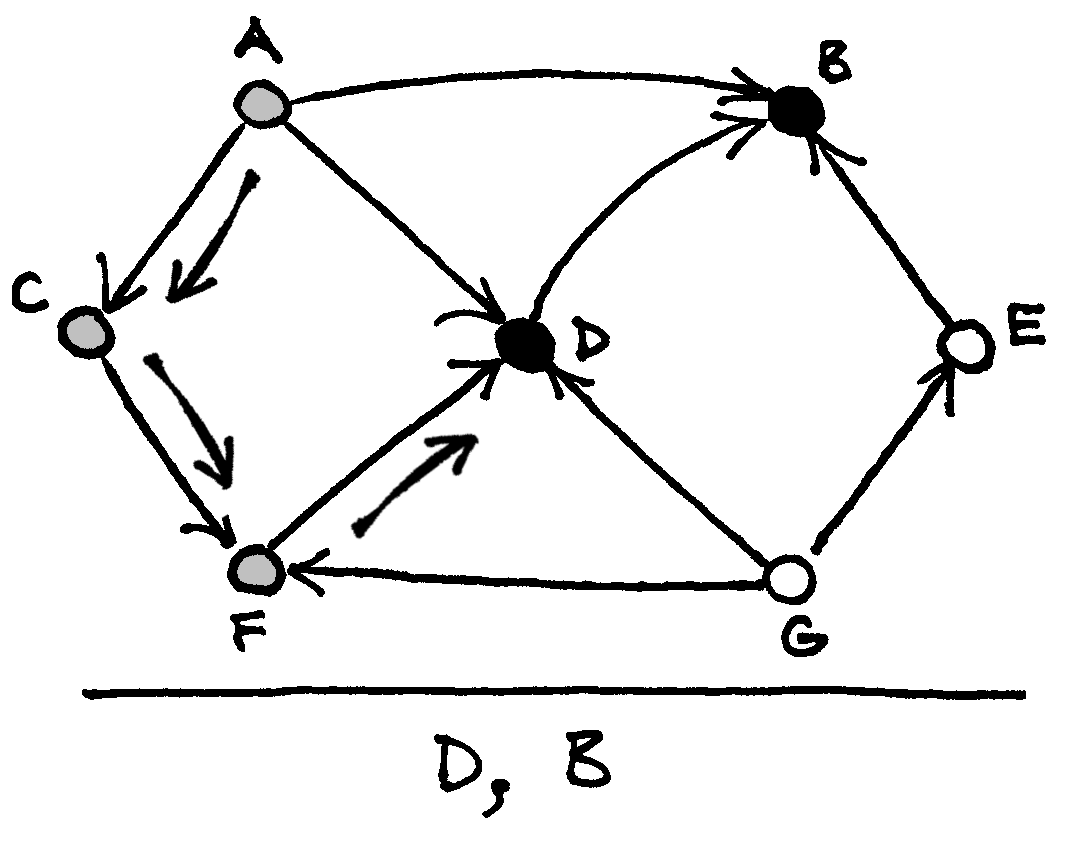
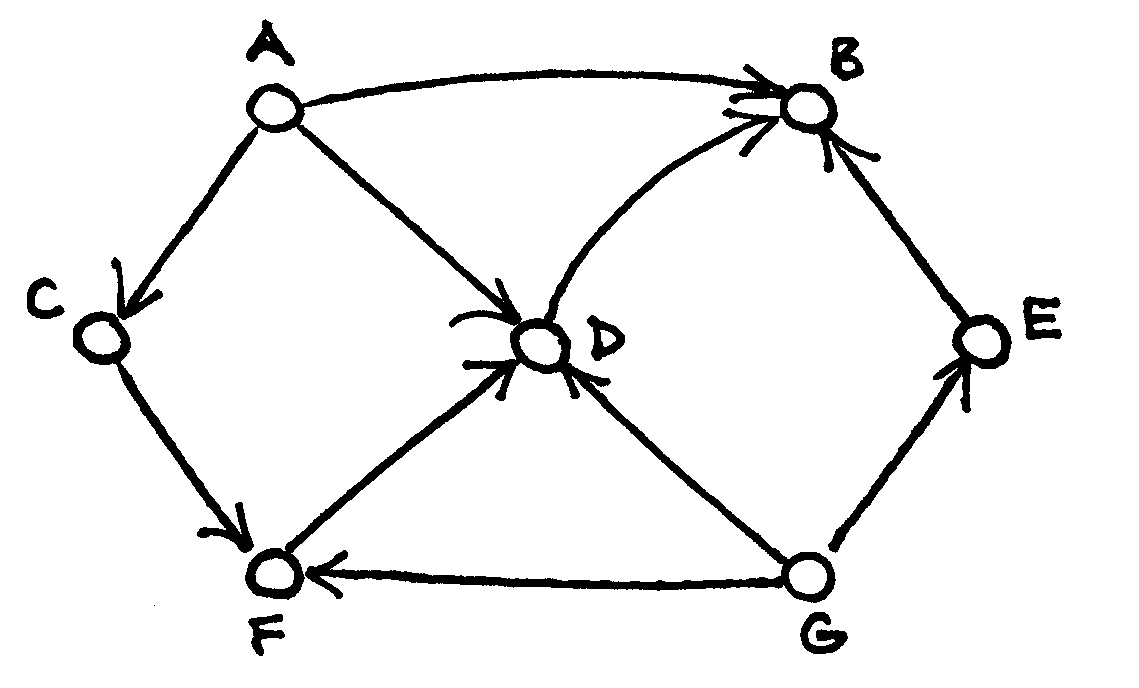
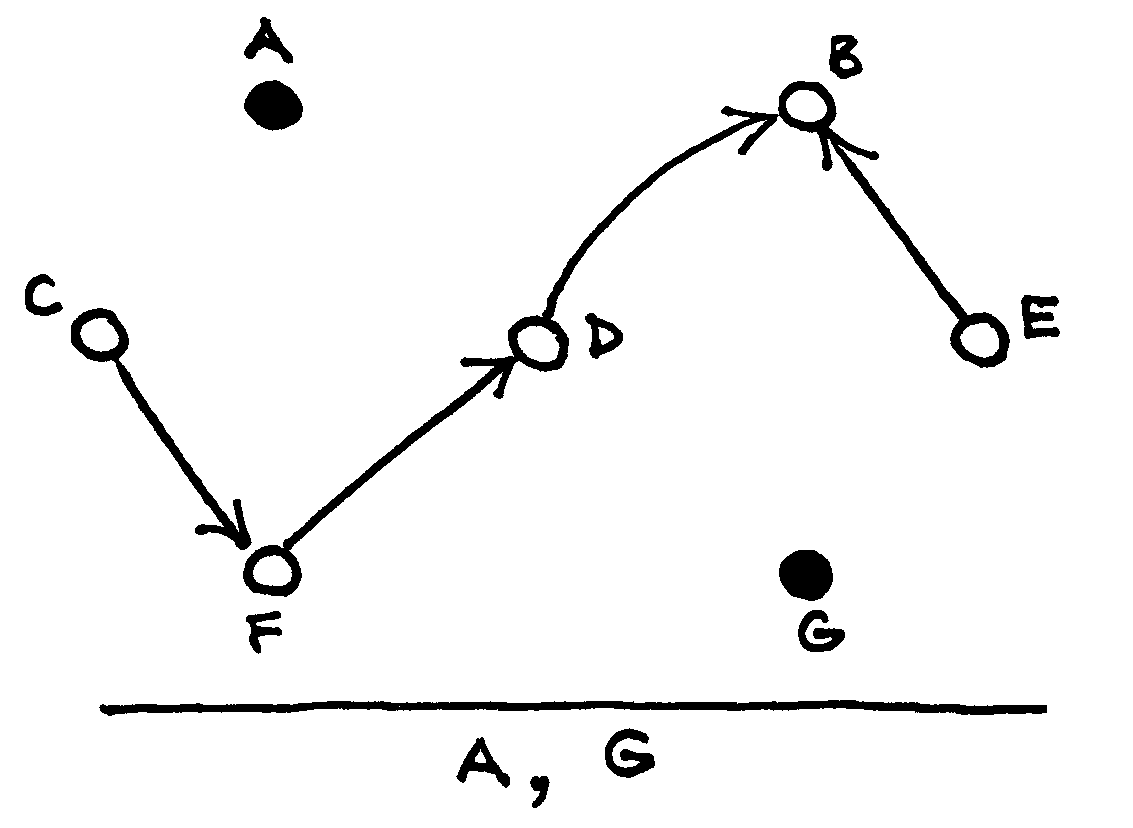
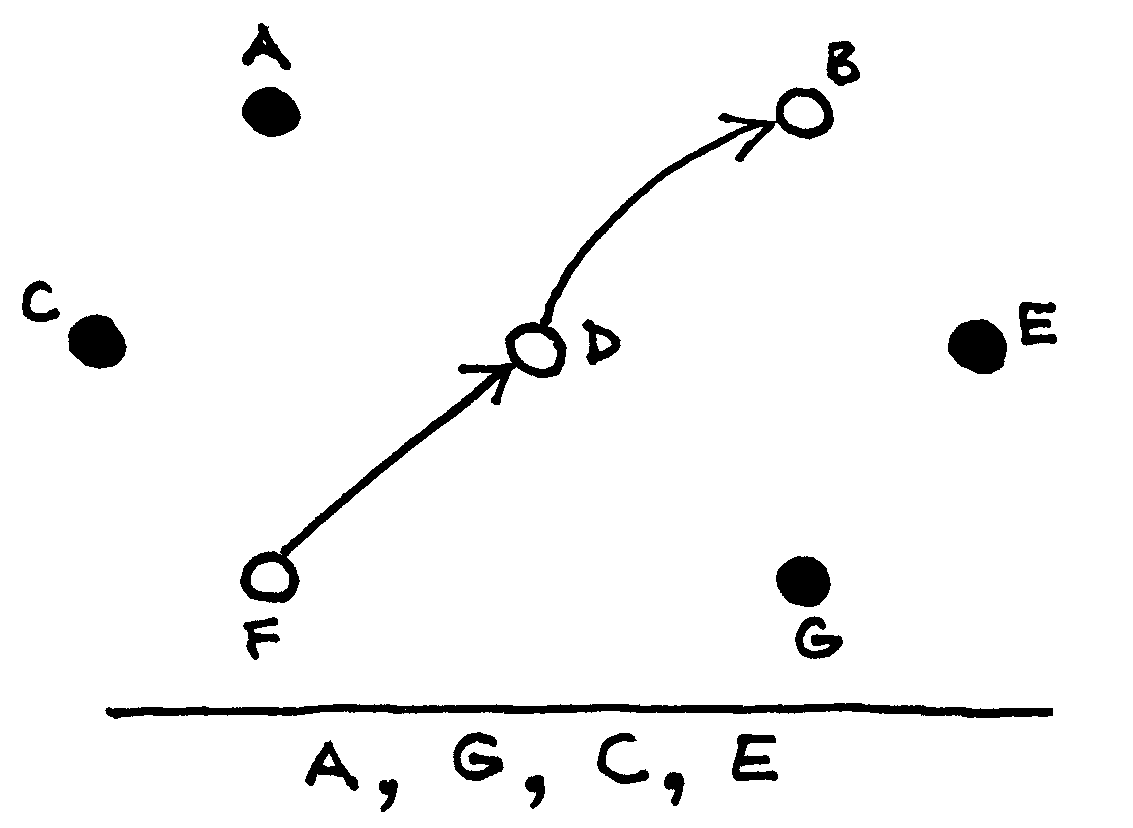
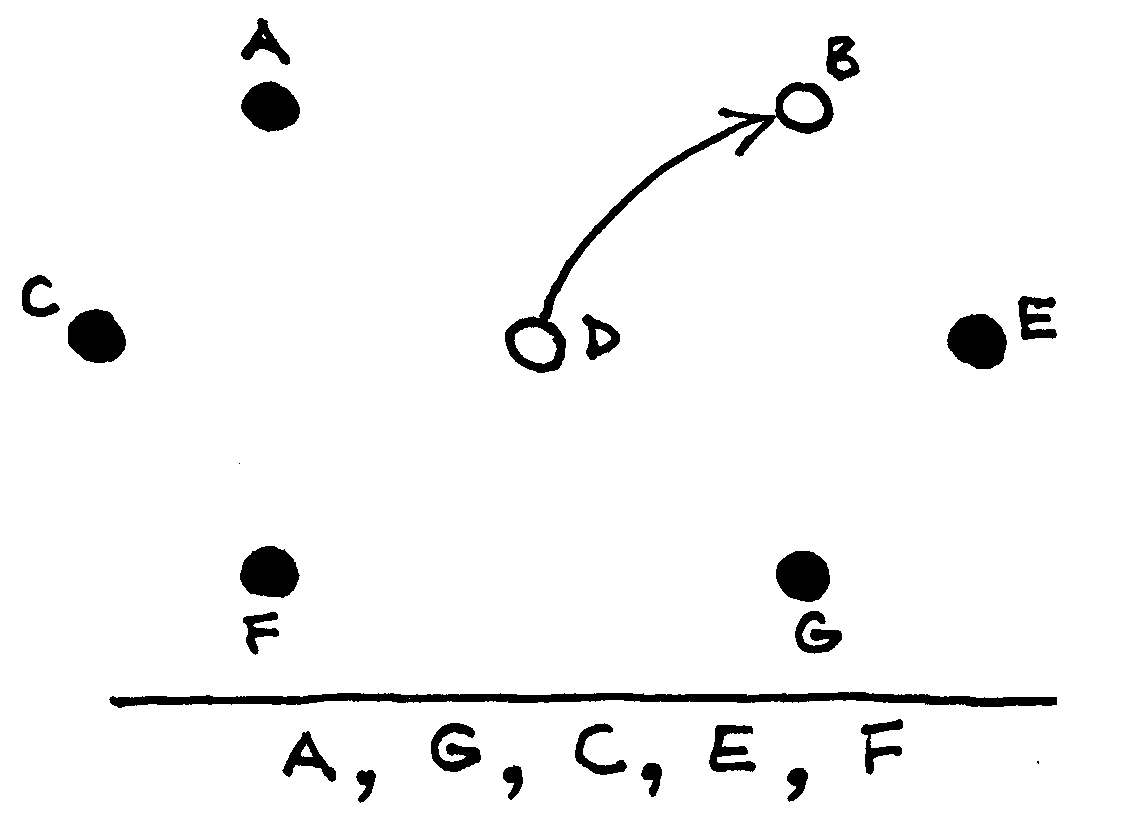
Žemiau pateikti paveikslai iliustruoja topologinį rikiavimą taikant paiešką gilyn.
Pradėjus nuo pasirinktos
viršūnės |
|
Jei baigus vykdyti paiešką gilyn lieka baltų viršūnių, tai pasirenkama bet kuri iš jų ir vėl vykdoma paieška gilyn |
Uždavinys Abėcėlė 1¶
Dauguma mūsų moka išrikiuoti žodžius pagal abėcėlę. Šiame uždavinyje nagrinėsime atvirkščią procesą. Duotas nežinomos kalbos žodžių, surikiuotų pagal tos kalbos abėcėlę, sąrašas. Į pateiktus žodžius įeina visos tos kalbos abėcėlės raidės.
Užduotis. Reikia rasti šios nežinomos kalbos abėcėlę.
Visos raidės rikiavimo ir abėcėlės požiūriu laikomos skirtingomis, taip pat trumpesnis žodis eina prieš ilgesnį žodį, gautą iš to trumpesnio prirašant raidžių jo pabaigoje. Pavyzdžiui, lietuvių kalboje žodis „aš“ eina prieš žodį „ašara“. Sąraše pakanka informacijos abėcėlei nustatyti.
Prisiminkime, ką kalbėjome apie olimpiadinius uždavinius, kurių sąlygose minimas rikiavimas: dažniausiai jų sprendimui žinomų rikiavimo algoritmų tiesiogiai pritaikyti negalėsime. Taip bus ir šį kartą. Nors sąlygoje kalbama apie rikiavimą, tai iš tiesų yra topologinio rikiavimo uždavinys.
Sakykime, žinome, kuris iš dviejų žodžių, išrikiavus abėcėlės tvarka, eina pirmas. Pavyzdžiui:
ARKLYSARKTINIS
Ką galime sužinoti apie raidžių tvarką abėcėlėje? Pirmosios skirtingos žodžių raidės yra L ir T, tad į jas ir buvo atsižvelgta rikiuojant žodžius. Vadinasi, nežinomoje abėcėlėje raidė L eina prieš raidę T.
Raides žymėsime grafo viršūnėmis, o sąryšius tarp raidžių –
lankais. Nustatę, kad raidė A abėcėlėje eina prieš raidę B,
nuvesime lanką iš viršūnės 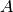 į viršūnę
į viršūnę 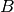 .
Gautasis grafas bus aibė reikalavimų, kuriuos turi tenkinti tos kalbos
raidžių tvarka abėcėlėje. Abėcėlę, tenkinančią šiuos
reikalavimus, rasime būtent topologiškai išrikiavę grafo viršūnes.
Uždavinio sąlyga teigia, jog sąraše pakanka informacijos raidžių
tvarkai nustatyti, taigi sudaryto grafo viršūnes bus įmanoma
topologiškai išrikiuoti vieninteliu būdu.
.
Gautasis grafas bus aibė reikalavimų, kuriuos turi tenkinti tos kalbos
raidžių tvarka abėcėlėje. Abėcėlę, tenkinančią šiuos
reikalavimus, rasime būtent topologiškai išrikiavę grafo viršūnes.
Uždavinio sąlyga teigia, jog sąraše pakanka informacijos raidžių
tvarkai nustatyti, taigi sudaryto grafo viršūnes bus įmanoma
topologiškai išrikiuoti vieninteliu būdu.
Sudarinėjant grafą, pakanka išnagrinėti tik gretimų sąrašo žodžių poras: jei žinoma, kad raidė A eina prieš raidę B, o raidė B prieš raidę C, tai šias raides topologiškai išrikiavus raidė A būtinai eis prieš raidę C. Pavyzdžiui, sudarykime grafą iš tokio rusų kalbos žodžių, išrikiuotų abėcėlės tvarka, sąrašo:
ЕМИМЯМАМАМЕНЯМНЕМОНЕТАНЕТНИНАОНАОНИРОТТОТЯ
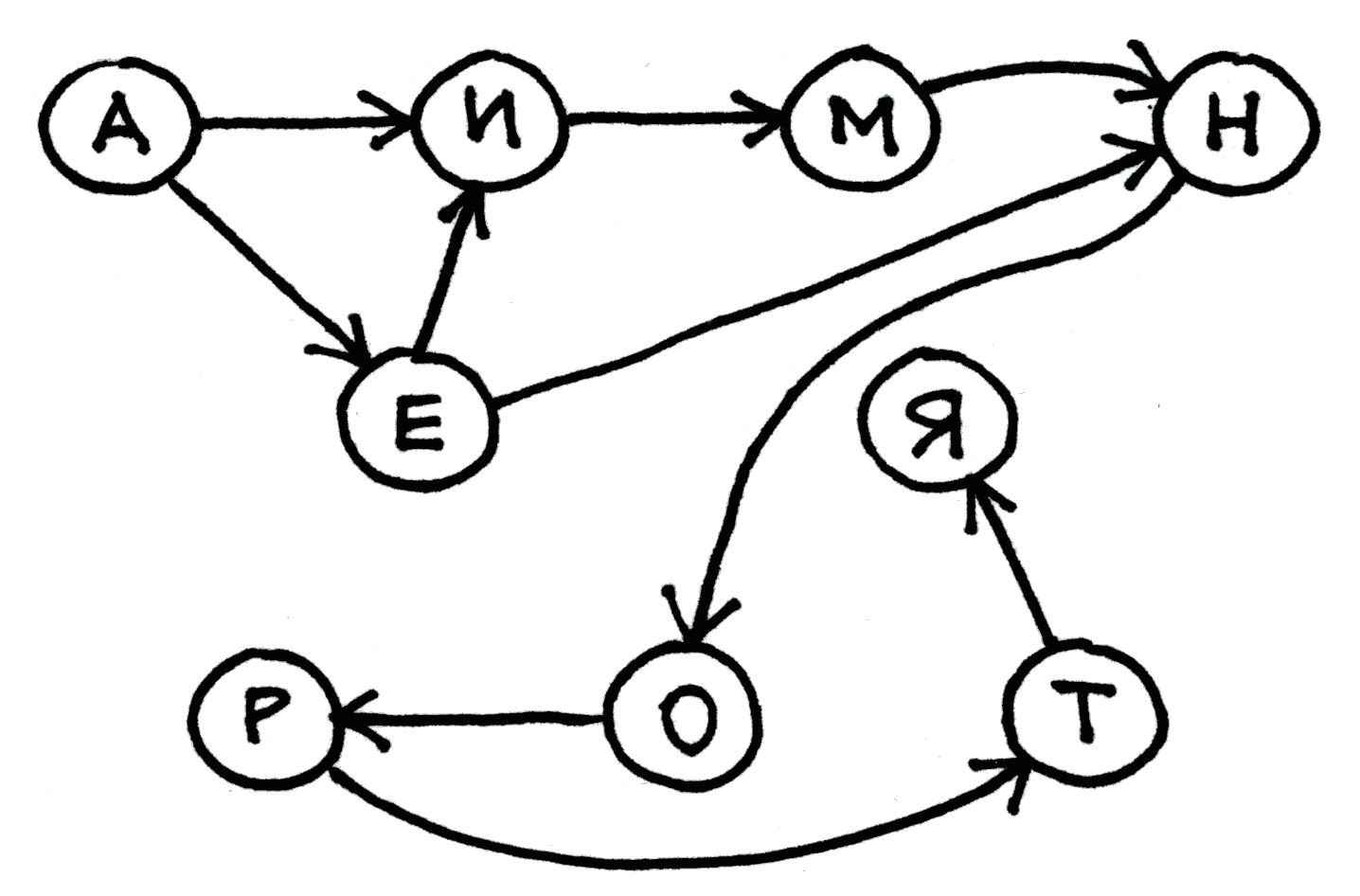
Fig. 58 Grafas, atitinkantis pateiktą žodžių sąrašą¶

Fig. 59 Topologiškai išrikiavę raidžių grafą, randame nežinomos kalbos abėcėlę¶
Žemiau pateiktame sprendime grafo struktūroje žymėsime, kurias
raides atitinkančios viršūnės yra grafe, nes ne visi simboliai
įeina į abėcėlę. Procedūrai rask_abėcėlę perduodamas
išrikiuotų pagal abėcėlę žodžių masyvas.
const MAXŽODŽIŲ = ...;
type žodžiai = array [1..MAXŽODŽIŲ + 1] of string;
grafas = record
n : integer; { viršūnių skaičius }
viršūnė : array [char] of boolean;
{ ar grafe yra raidę atitinkanti viršūnė }
lankas : array [char, char] of boolean;
įein_lankų : array [char] of integer;
end;
procedure rask_abėcėlę(sk : integer; { žodžių skaičius }
var ž : žodžiai;
var abėcėlė : string);
{ atsakymas įrašomas į eilutę abėcėlė }
procedure sudaryk_grafą(var g : grafas);
var i, j, m : integer;
c, d : char;
begin
{ išvalomi masyvai }
g.n := 0;
for c := low(char) to high(char) do begin
g.viršūnė[c] := false;
g.įein_lankų[c] := 0;
for d := low(char) to high(char) do
g.lankas[c, d] := false;
end;
{ sudaromas grafas }
ž[sk + 1] := ''; { pridedame tuščią žodį }
for i := 1 to sk do begin
{ jei randama naujų raidžių – jos įtraukiamos į grafą }
for j := 1 to length(ž[i]) do
if not g.viršūnė[ž[i][j]] then begin
g.viršūnė[ž[i][j]] := true;
inc(g.n);
end;
m := min (length(ž[i]), length(ž[i + 1]));
{ Funkcijos min teksto nepateikiame – ji
paprasčiausiai grąžina mažesnįjį iš dviejų
parametrų. }
j := 1;
while (j <= m) and (ž[i][j] = ž[i+1][j])
do inc(j); { ieškoma nesutampanti raidė }
if (j <= m) and
not g.lankas[ž[i][j], ž[i+1][j]]
then begin
{ rasta nesutampanti raidė – grafas papildomas lanku }
g.lankas[ž[i][j], ž[i+1][j]] := true;
inc(g.įein_lankų[ž[i + 1][j]]);
end;
end;
end;
var g : grafas;
c, d : char;
begin
sudaryk_grafą(g);
{ topologiškai išrikiuojamas grafas (randama abėcėlė) }
abėcėlė := '';
while g.n > 0 do begin
c := low(char);
{ randama viršūnė be įeinančių lankų }
while (not g.viršūnė[c]) or
(g.įein_lankų[c] > 0) do inc(c);
{ raidė pridedama prie abėcėlės }
abėcėlė := abėcėlė + c;
{ atnaujinami kaimynių laipsniai }
for d := low(char) to high(char) do
if g.lankas[c, d] then
dec(g.įein_lankų[d]);
{ viršūnė ištrinama iš grafo }
g.viršūnė[c] := false;
dec(g.n);
end;
end;
#include <limits.h>
/*
šios bibliotekos prireiks, kadangi naudosime konstantas
CHAR_MIN (mažiausia char tipo kintamojo pasiekiama reikšmė) ir
CHAR_MAX (didŽiausia char tipo kintamojo pasiekiama reikšmė)
*/
const int MAXZODZIU = ...;
int sk; // žodžių skaičius
string z[MAXZODZIU + 1]; // žodžių masyvas
int n; // viršūnių skaičius
map<char, bool> virsune; // ar grafe yra raidę atitinkanti viršūnė
map<pair<char, char>, bool> lankas;
map<char, int> ieinLanku;
void sudarykGrafa () {
// išvalomos duomenų struktūros
n = 0;
virsune.clear();
lankas.clear();
ieinLanku.clear();
// sudaromas grafas
zodziai[sk] = ""; // pridedame tuščią žodį
for (int i = 0; i < sk; i++) {
for (int j = 0; j < (int)z[i].size(); j++) {
// jei randama naujų raidžių - jos įtraukiamos į grafą
if (!virsune[z[i][j]]) {
n++;
virsune[z[i][j]] = true;
}
}
int m = min((int)z[i].size(), (int)z[i+1].size());
int j = 0;
while (j < m && z[i][j] == z[i+1][j]) {
j++;
// ieškoma nesutampanti raidė
}
if (j < m && !(lankas[{z[i][j], z[i+1][j]}])) {
// rasta nesutampanti raidė - grafas papildomas lanku
lankas[{z[i][j], z[i+1][j]}] = true;
ieinLanku[z[i+1][j]]++;
}
}
}
string raskAbecele () {
string abecele = ""; // atsakymas bus įrašomas į eilutę "abėcėlė"
sudarykGrafa (); // topologiškai išrikiuojamas grafas (randama abėcėlė)
while (n > 0) {
char c = CHAR_MIN;
// randama viršūnė be įeinančių lankų
while (!virsune[c] || ieinLanku[c] > 0) {
c++;
}
abecele += c; // raidė pridedama prie abėcėlės
// atnaujinami kaimynų laipsniai
for (char d = CHAR_MIN; d <= CHAR_MAX; d++) {
if (lankas[{c,d}])
ieinLanku[d]--;
// viršūnė ištrinama iš grafo
virsune[c] = false;
n--;
}
return abecele;
}
Atkreipiame dėmesį, kad šio uždavinio sprendime topologinis
rikiavimas realizuotas kitaip – grafas vaizduojamas kaimynystės
matrica, nenaudojama eilės duomenų struktūra. Algoritmo sudėtingumas
– 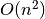 .
.
Išnašos
- 1
Analogiškas uždavinys buvo pateiktas Lietuvos informatikos olimpiados III etape 2005 metais.
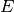 , kurių laipsniai
tapo lygūs 0
, kurių laipsniai
tapo lygūs 0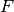 , nes jos
laipsnis lygus 0; viršūnė
, nes jos
laipsnis lygus 0; viršūnė