Medžiai, Minimalaus jungiamojo medžio radimas¶
I hope to convince you that mathematical trees are no less lovely thantheir biological counterparts.Tikiuosi, galiausiai jūs sutiksite, jog matematiniai medžiaidžiugina širdį ne mažiau nei tikrieji.Džo Malkevičius (Joe Malkevitch)
Ankstesniuose skyriuose išplėtėme grafo sąvoką: susipažinome su orientuotais bei svoriniais grafais. Šį kartą susiaurinsime grafo sąvoką. Panagrinėsime medžius – grafus, pasižyminčius tam tikromis savybėmis. Pamatysime, jog medžiai dažnai pasitaiko, kai grafais modeliuojami praktiniai uždaviniai.
Medžiai¶
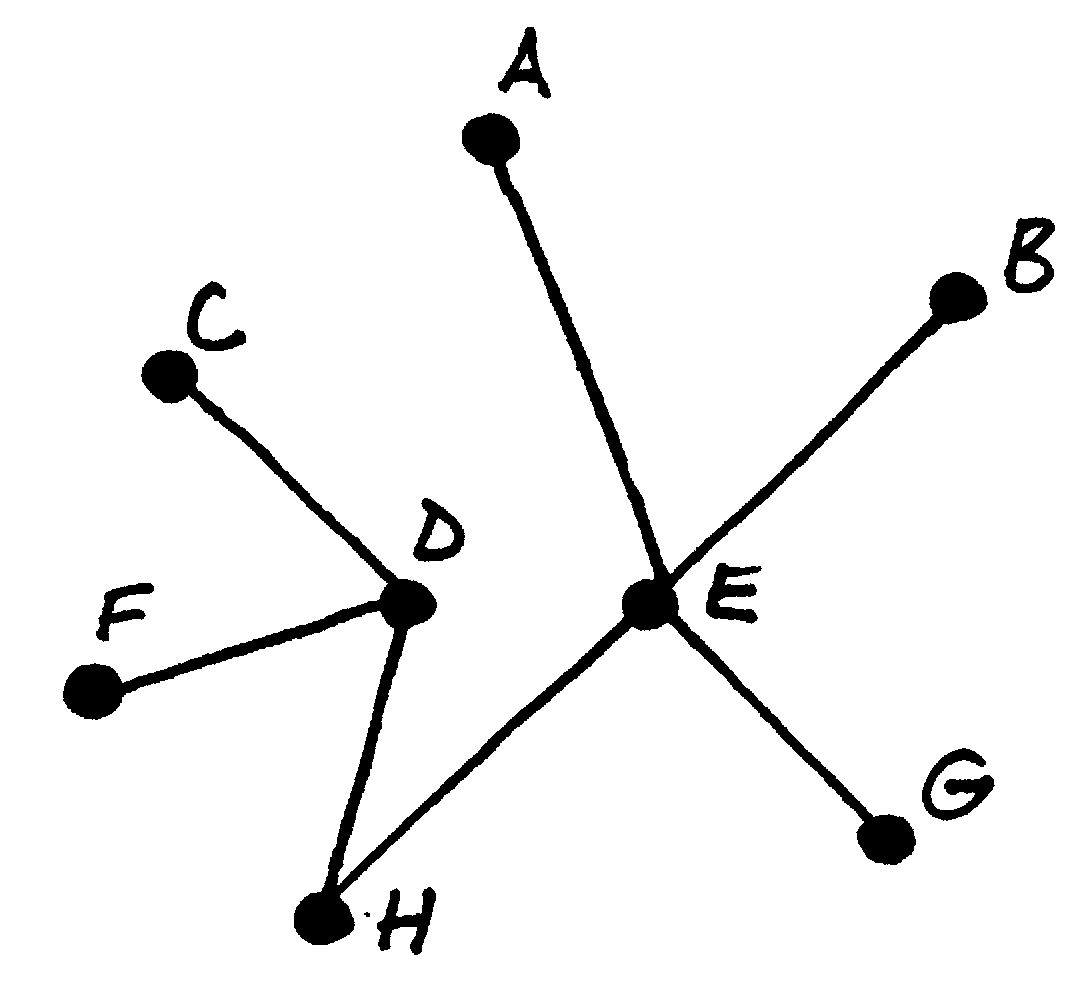
Fig. 63 Medis¶
Medžiu vadinamas neorientuotas jungus ciklų neturintis grafas.
Kiekvienas medis pasižymi tokiomis savybėmis:
bet kurias dvi viršūnes medyje jungia vienintelis kelias;
visos medžio briaunos yra tiltai (t. y. panaikinus bet kurią briauną medis taptų nejungus);
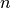 viršūnių turintis medis visuomet turi
viršūnių turintis medis visuomet turi 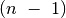 briauną, ir atvirkščiai – jungusis grafas turintis
briauną, ir atvirkščiai – jungusis grafas turintis 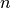 viršūnių ir
viršūnių ir 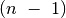 briauną yra medis.
briauną yra medis.
Kai kada medžiuose viena viršūnė išskiriama iš kitų ir pavadinama medžio šaknimi, o pats medis – šakniniu medžiu.
Šakninio medžio viršūnės taip pat turi skirtingus pavadinimus. Bet
kuri viršūnė 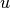 , esanti tiesioginiame kelyje tarp šakninės
viršūnės ir viršūnės
, esanti tiesioginiame kelyje tarp šakninės
viršūnės ir viršūnės  , vadinama viršūnės
, vadinama viršūnės  protėviu, o viršūnė
protėviu, o viršūnė  vadinama viršūnės
vadinama viršūnės 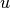 vaikaičiu. Šakninė viršūnė yra visų medžio viršūnių
protėvis, o visos medžio viršūnės yra jos vaikaičiai, kiekviena
viršūnė yra savo pačios protėvis ir vaikaitis. Jei viršūnė
vaikaičiu. Šakninė viršūnė yra visų medžio viršūnių
protėvis, o visos medžio viršūnės yra jos vaikaičiai, kiekviena
viršūnė yra savo pačios protėvis ir vaikaitis. Jei viršūnė
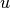 yra
yra  protėvis ir egzistuoja briauna, jungianti
protėvis ir egzistuoja briauna, jungianti
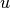 ir
ir  , tuomet
, tuomet 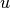 vadinama pirmine (tėvine)
vadinama pirmine (tėvine)
 viršūne, o
viršūne, o  vadinama antrine (vaikine)
vadinama antrine (vaikine)
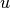 viršūne. Medžio viršūnė, neturinti antrinių
viršūnių, vadinama lapu.
viršūne. Medžio viršūnė, neturinti antrinių
viršūnių, vadinama lapu.
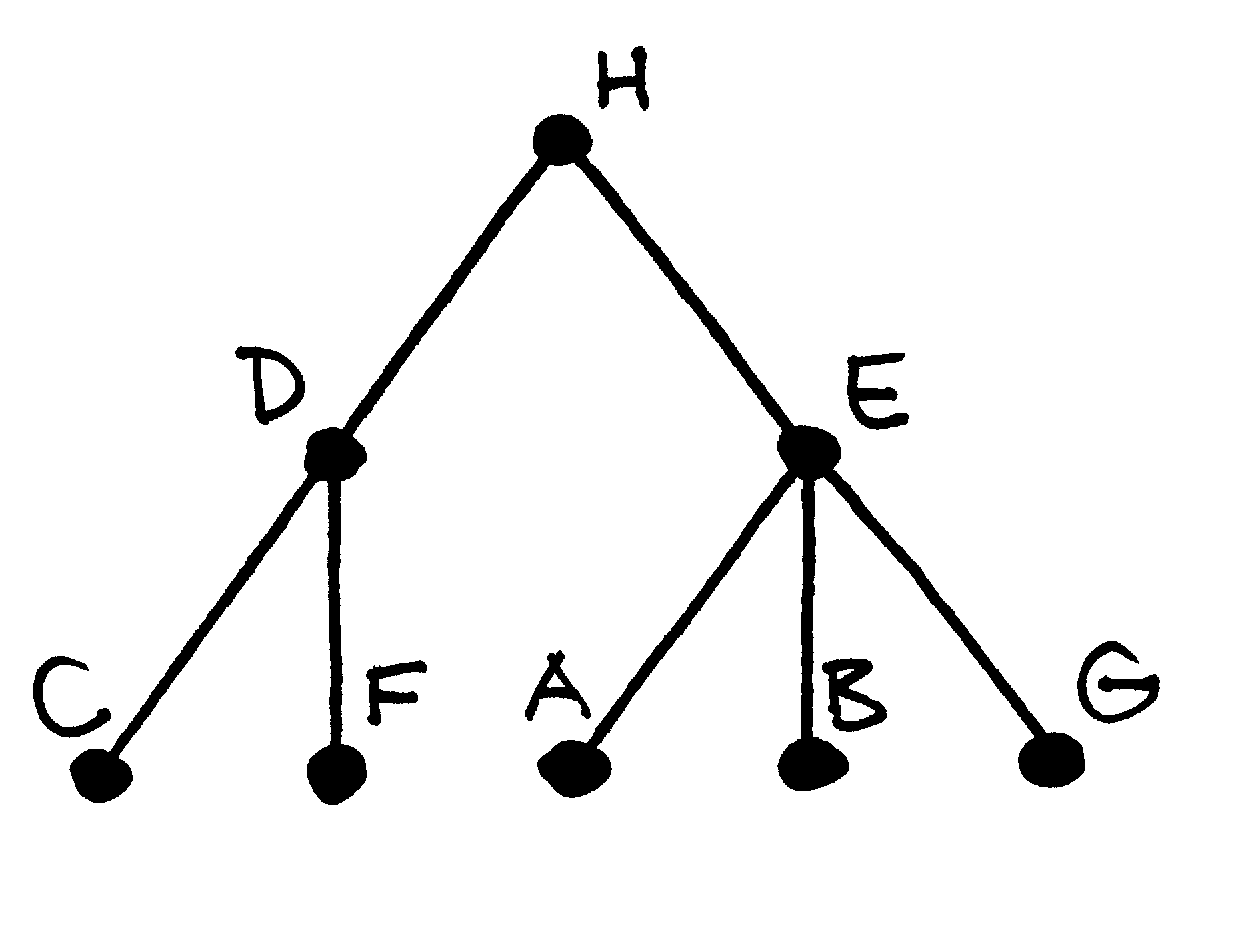
Fig. 64 Šakninis medis, gautas iš praeitame paveiksle pateikto
medžio, šaknine pasirinkus viršūnę 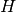 ; medis turi penkis
lapus
; medis turi penkis
lapus 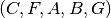 ; šakninė viršūnė
; šakninė viršūnė 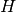 turi dvi
antrines viršūnes (
turi dvi
antrines viršūnes (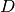 ir
ir 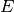 ) ir 7 vaikaičius
) ir 7 vaikaičius
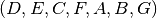 .¶
.¶
Medžių vaizdavimas¶
Medis yra susiaurinta grafo sąvoka: bet kuris medis yra grafas, bet ne
atvirkščiai. Tad medžius galima vaizduoti lygiai tomis pačiomis
duomenų struktūromis kaip ir grafus: kaimynystės matricomis ir
kaimynystės sąrašais. Kita vertus, galime tikėtis rasti
elegantiškesnį būdą medžiams pavaizduoti. Juk iš anksto žinome,
jog toks grafas turės 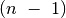 briauną, bus jungus bei
neturės ciklų.
briauną, bus jungus bei
neturės ciklų.
Iš tiesų, jei medis šakninis, tai kiekviena viršūnė, išskyrus medžio šaknį, turi lygiai vieną pirminę viršūnę. Todėl medį visiškai apibrėžia jau anksčiau minėtas pirminumo masyvas:
const MAX = ...; { maksimalus medžio viršūnių skaičius }
type masyvas = array [1..MAX] of integer;
var pirminė : masyvas; { kiekvienai viršūnei įsimenama jos
pirminė viršūnė }
const int MAXN = ...; // maksimalus medžio viršūnių skaičius
int pirmine[MAXN]; // kiekvienai viršūnei įsimenama jos pirminė viršūnė
Taip pavaizdavę medį, galime sužinoti visas medžiui priklausančias
briaunas (jos yra pavidalo (k, pirminė[k])) ir efektyviai
rasti kelius nuo viršūnės  iki šakninės viršūnės,
pereinant visus viršūnės
iki šakninės viršūnės,
pereinant visus viršūnės  protėvius. Tačiau „leistis“
medžiu, t. y. ieškoti kiekvienos viršūnės antrinių viršūnių
efektyviai negalime, nes tektų peržiūrėti visą masyvą.
protėvius. Tačiau „leistis“
medžiu, t. y. ieškoti kiekvienos viršūnės antrinių viršūnių
efektyviai negalime, nes tektų peržiūrėti visą masyvą.
Siekdami efektyviai rasti tiek pirminę, tiek ir antrines viršūnes, šakninį medį galime vaizduoti įrašų masyvu, kuriame saugoma kiekvienos viršūnės pirminė viršūnė ir antrinių viršūnių sąrašas:
type viršūnė = record
pirminė : integer;
antr_sk : integer; { antrinių viršūnių skaičius }
antr_sąr : array [1..MAX] of integer
end;
medis = array [1..MAX] of viršūnė;
int pirmine[MAXN];
vector<int> antrSar[MAXN]; // antrinių viršūnių sąrašas
Toks vaizdavimas neefektyvus atminties požiūriu: nors visų
viršūnių sąrašų antr_sąr ilgių suma bus lygi
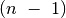 , šiems masyvams skiriama
, šiems masyvams skiriama 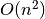 atminties,
nes iš anksto nežinoma, kiek kuri viršūnė turės antrinių. Šią
problemą galima spręsti naudojant dinaminę atmintį, kuomet atmintis
išskiriama tik tada, kai jos prireikia, ir kiekvienam sąrašui
išskirti tik tiek atminties, kiek būtina. Tačiau dinaminės duomenų
struktūros yra gana sudėtingos, jų realizavimas ir derinimas atima
nemažai laiko, todėl olimpiadose geriau jų vengti.
atminties,
nes iš anksto nežinoma, kiek kuri viršūnė turės antrinių. Šią
problemą galima spręsti naudojant dinaminę atmintį, kuomet atmintis
išskiriama tik tada, kai jos prireikia, ir kiekvienam sąrašui
išskirti tik tiek atminties, kiek būtina. Tačiau dinaminės duomenų
struktūros yra gana sudėtingos, jų realizavimas ir derinimas atima
nemažai laiko, todėl olimpiadose geriau jų vengti.
Kokį vaizdavimą pasirinkti? Tai visuomet priklauso nuo sprendžiamo uždavinio. Dažnai pakanka medį saugoti pirminumo masyvu. Kai norima efektyviai ieškoti antrinių viršūnių, medį tenka vaizduoti antruoju būdu, jei tik viršūnių skaičius nėra per didelis. Be to, kai kuriuose uždaviniuose nagrinėjami specifiniai medžiai, pavyzdžiui, kurių kiekviena viršūnė turi ne daugiau kaip dvi antrines viršūnes (dvejetainiai medžiai). Jiems nesunku pritaikyti įrašo tipo struktūrą.
Minimalus jungiamasis medis¶
Panagrinėsime optimizavimo uždavinį, su kuriuo dažnai susiduriama
praktikoje. Tarkime, kad tiesiamos elektros linijos tiekti elektrai į
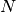 miestelių. Šiuo tikslu visus N miestelių reikia sujungti į
vieną elektros tinklą. Yra apskaičiuota linijos nutiesimo tarp bet
kurių dviejų miestelių kaina, ir norima sudaryti tokį elektros
linijų planą, kad visų linijų tiesimo kainų suma būtų kuo
mažesnė. Be abejo, nutiesus linijas, kiekvienas miestelis turi turėti
elektrą.
miestelių. Šiuo tikslu visus N miestelių reikia sujungti į
vieną elektros tinklą. Yra apskaičiuota linijos nutiesimo tarp bet
kurių dviejų miestelių kaina, ir norima sudaryti tokį elektros
linijų planą, kad visų linijų tiesimo kainų suma būtų kuo
mažesnė. Be abejo, nutiesus linijas, kiekvienas miestelis turi turėti
elektrą.
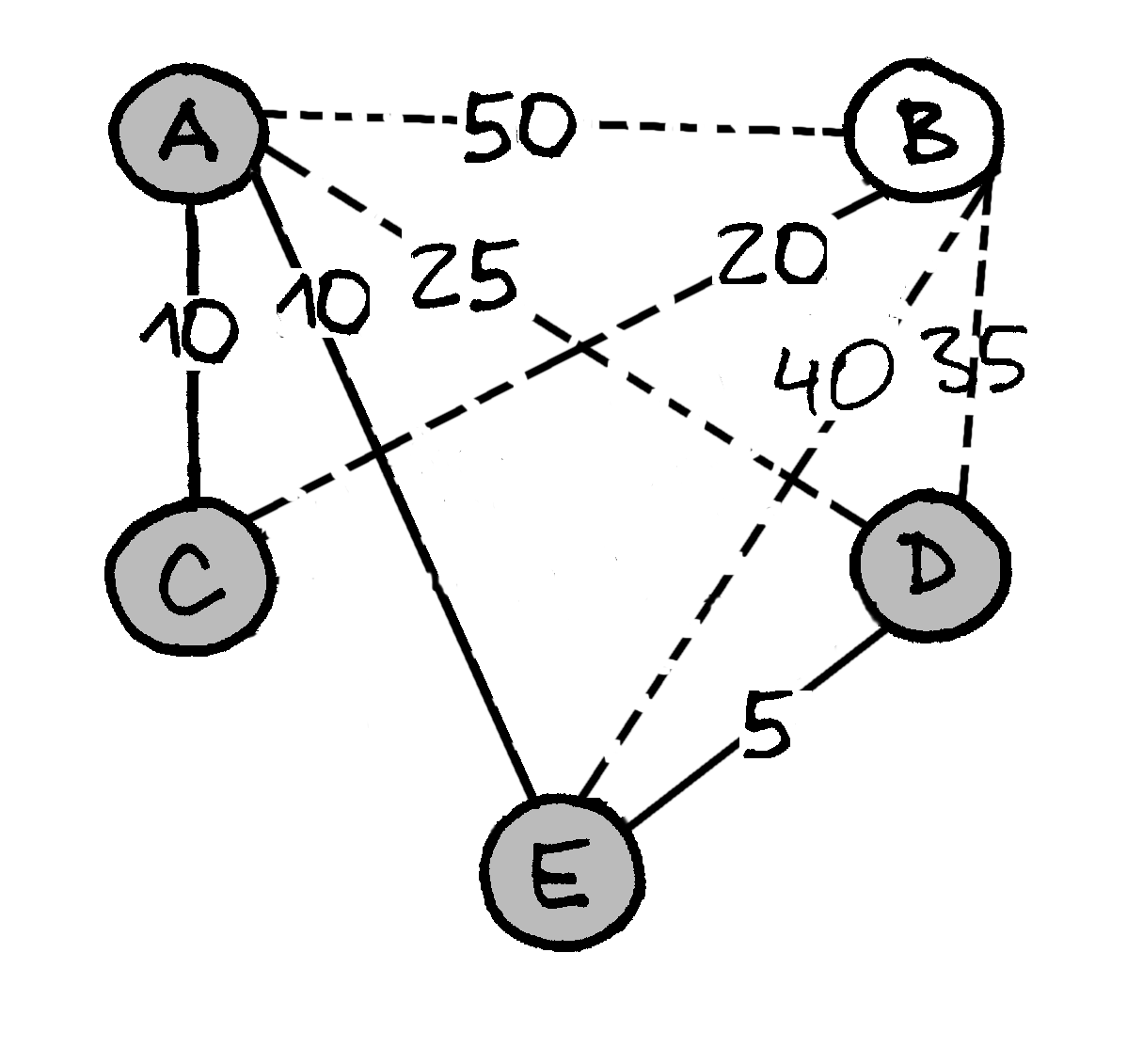
Panagrinėkime pavyzdį. Tarkime, kad miestelių yra penki, o elektros linijų tiesimo tarp miestelių porų kainos yra tokios:
A |
B |
C |
D |
E |
|
A |
– |
50 |
10 |
25 |
10 |
B |
50 |
– |
20 |
35 |
40 |
C |
10 |
20 |
– |
15 |
24 |
D |
25 |
35 |
15 |
– |
5 |
E |
10 |
40 |
24 |
5 |
– |
Paveiksluose pateikiami keli elektros linijų tiesimo planai.
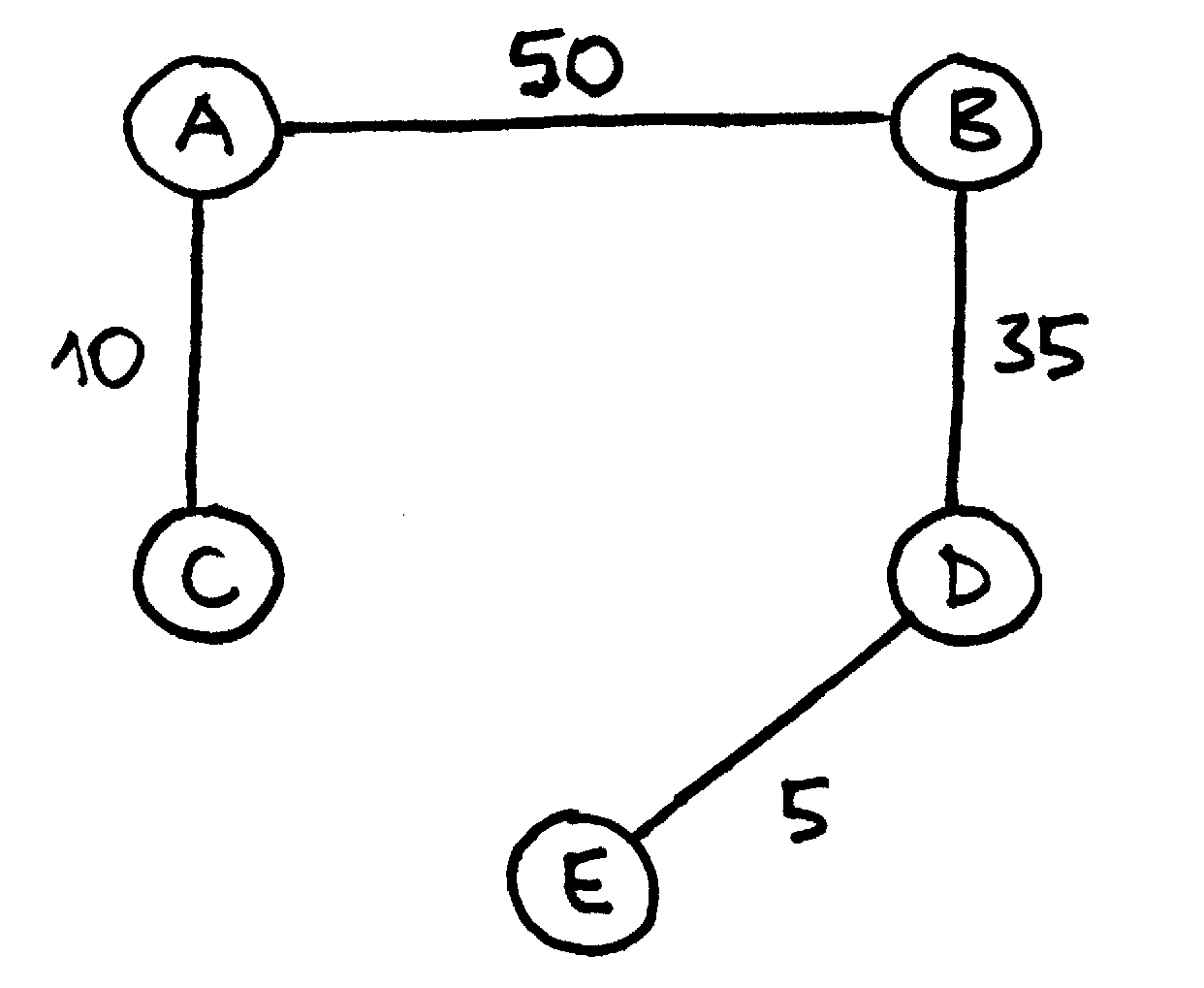
Fig. 65 Pirmas visų penkių miestelių sujungimo būas; tokio sujungimo kaina – 100¶
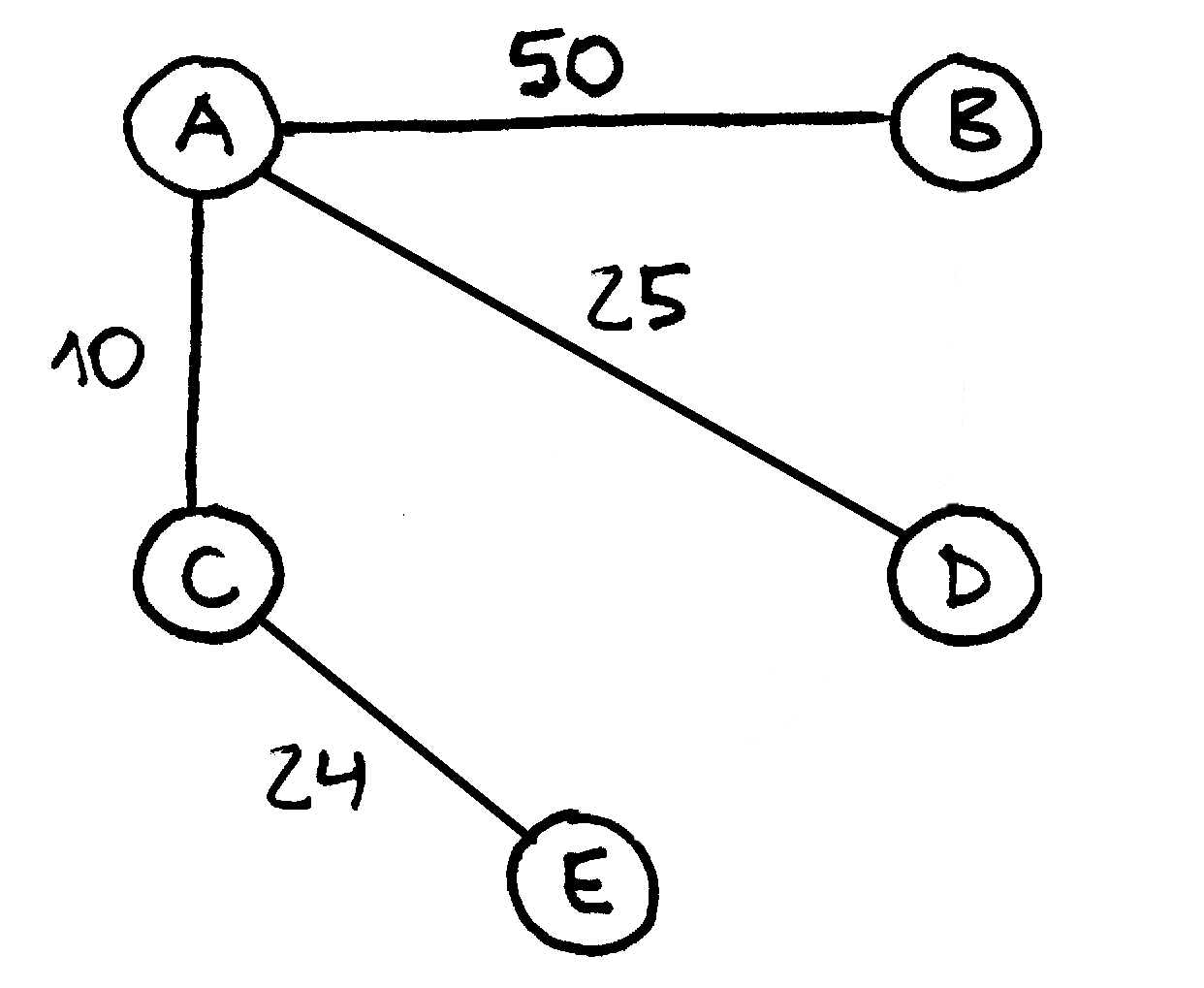
Fig. 66 Antras miestelių sujungimo būdas; šio sujungimo kaina – 109¶
Matyti, kad yra ne vienas būdas sujungti miestelius į tinklą, ir vieni šių būdų gali būti ekonomiškesni už kitus.
Turbūt jau supratote, jog šį uždavinį nesunku formaliai apibrėžti grafų teorijos terminais. Tačiau prieš tai įvesime dar kelias sąvokas.
Grafo 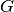 pografiu vadinamas grafas
pografiu vadinamas grafas 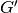 , kurį
papildžius viršūnėmis ir (arba) briaunomis, gaunamas grafas
, kurį
papildžius viršūnėmis ir (arba) briaunomis, gaunamas grafas
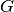 . Pografis
. Pografis 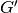 negali turėti briaunos arba viršūnės,
kurios neturi grafas
negali turėti briaunos arba viršūnės,
kurios neturi grafas 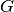 .
.
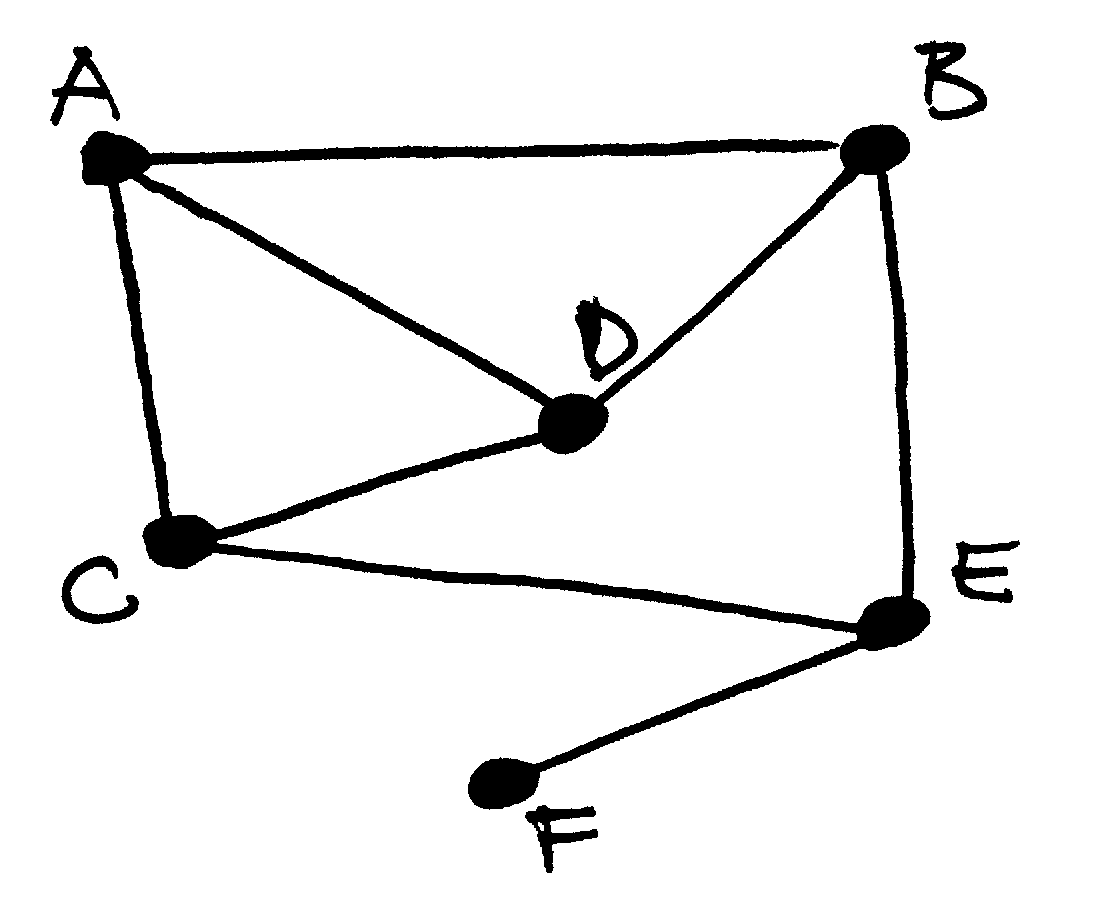
Fig. 67 Grafas¶
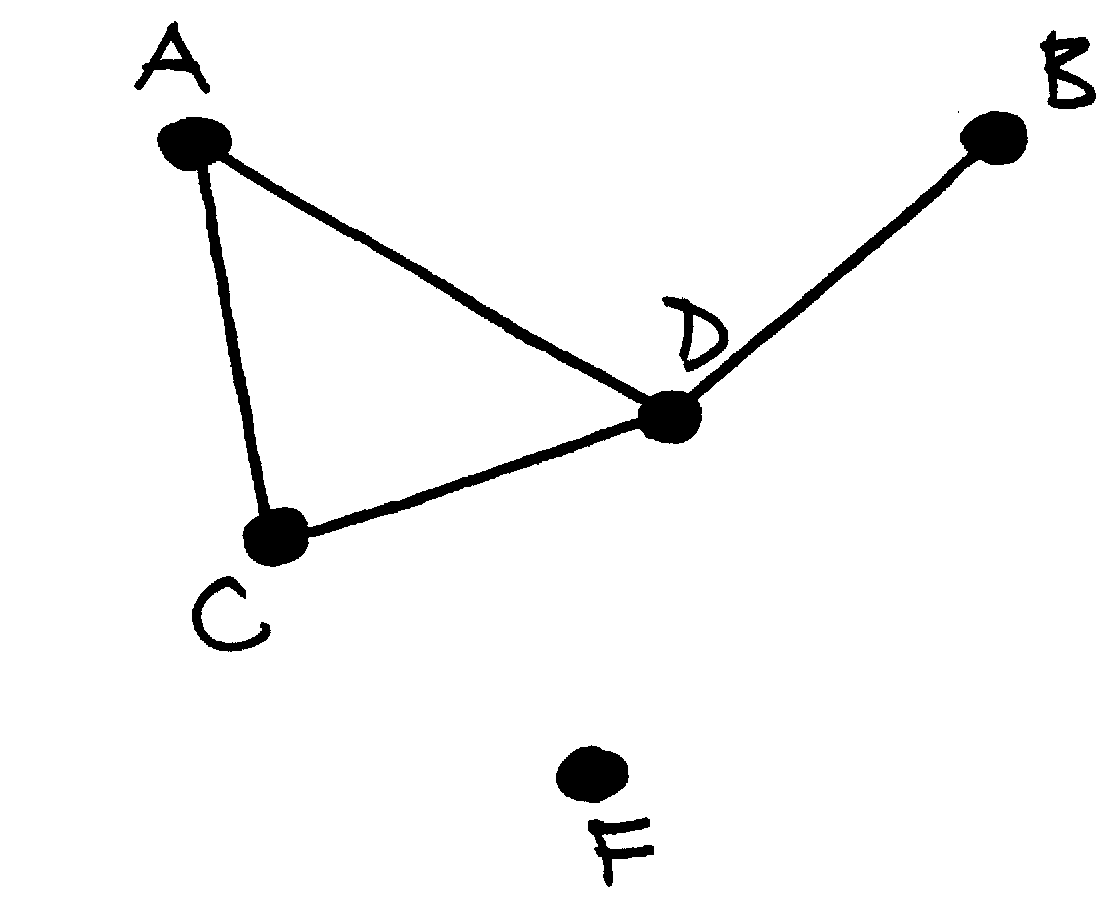
Fig. 68 Vienas iš aukščiau pateikto grafo pografių¶
Grafo 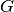 pografis, kuriam priklauso visos
pografis, kuriam priklauso visos 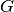 viršūnės
ir kuris yra medis, vadinamas grafo
viršūnės
ir kuris yra medis, vadinamas grafo 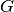 jungiamuoju medžiu.
Nesunku suvokti, kad vienas grafas gali turėti daugiau nei vieną
jungiamąjį medį. Tačiau jei grafas nejungus, jis neturi jungiamojo
medžio.
jungiamuoju medžiu.
Nesunku suvokti, kad vienas grafas gali turėti daugiau nei vieną
jungiamąjį medį. Tačiau jei grafas nejungus, jis neturi jungiamojo
medžio.
Dabar žinome viską, ko reikia nagrinėjamam uždaviniui formalizuoti.
Jei kiekvieną miestelį atitinka grafo 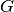 viršūnė, o elektros
linijos tiesimo iš miestelio
viršūnė, o elektros
linijos tiesimo iš miestelio 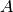 į miestelį
į miestelį 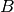 kainą
žymi briaunos
kainą
žymi briaunos 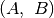 svoris, tai ieškomasis linijų tiesimo
planas yra grafo
svoris, tai ieškomasis linijų tiesimo
planas yra grafo 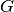 jungiamasis medis, kurio briaunų svorių
suma mažiausia. Toks medis vadinamas minimaliu jungiamuoju medžiu
(MJM), o pats uždavinys – minimalaus jungiamojo medžio uždaviniu.
jungiamasis medis, kurio briaunų svorių
suma mažiausia. Toks medis vadinamas minimaliu jungiamuoju medžiu
(MJM), o pats uždavinys – minimalaus jungiamojo medžio uždaviniu.
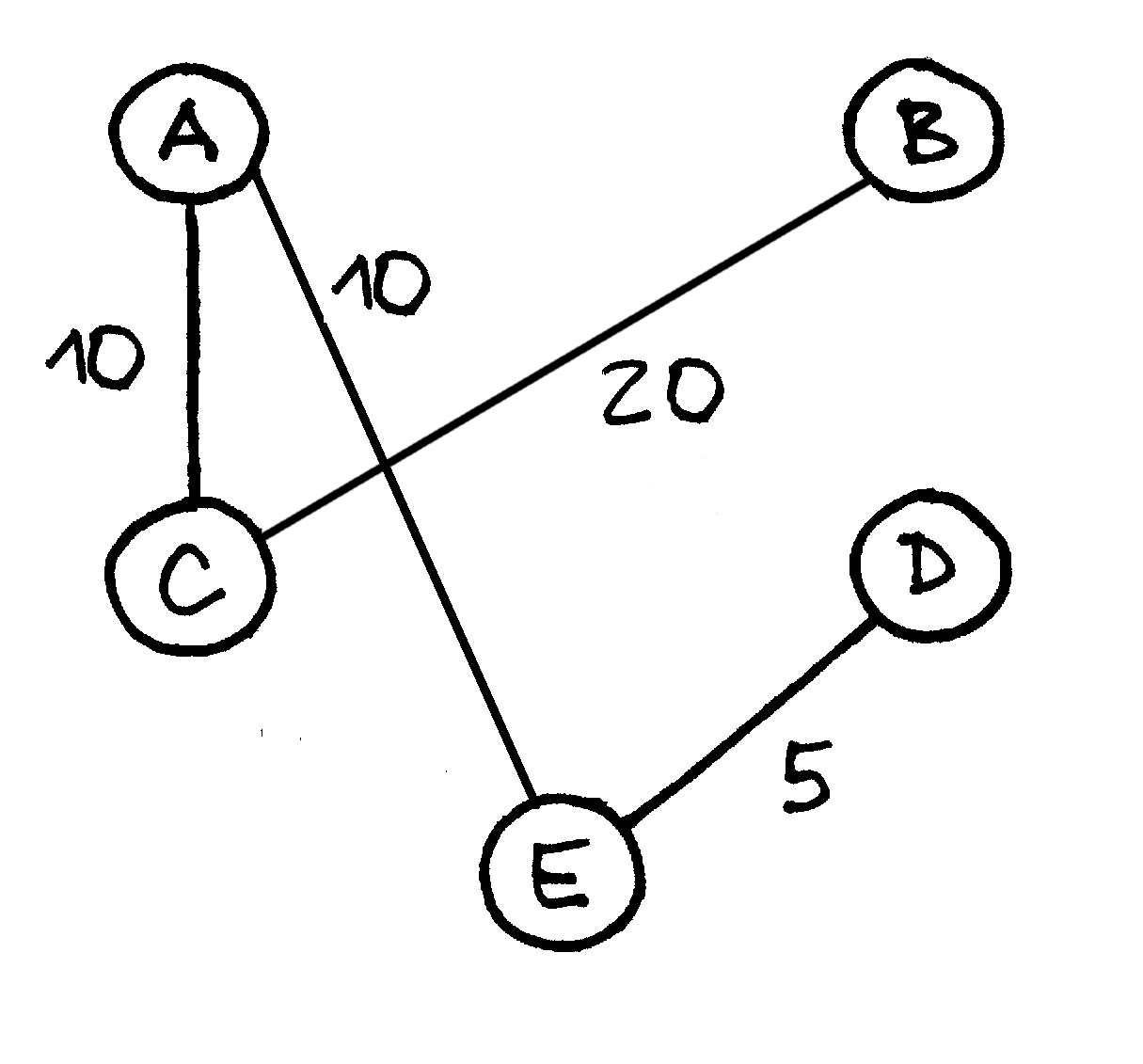
Fig. 69 Grafo, sudaryto iš skyrelio pradžioje nagrinėto pavyzdžio, minimalus jungiamasis medis; sujungimo kaina – 45¶
Kitame skyrelyje panagrinėsime efektyvius algoritmus minimalaus jungiamojo medžio paieškai.
Primo ir kiti algoritmai MJM rasti¶
Knygose ir mokslinėje literatūroje ilgą laiką buvo rašoma, kad pirmieji MJM ieškančius algoritmus sukūrė Džozefas Bernardas Kruskalas (Joseph Bernard Kruskal) ir Robertas Klėjus Primas (Robert Clay Prim) apie 1956–1957 metus. Šie algoritmai vėliau buvo pavadinti jų vardais. Deja, liko nepastebėta, kad labai gražų ir elegantišką algoritmą MJM paieškai net dvidešimčia metų anksčiau jau siūlė čekų mokslininkas Otakaras Boruvka (Otakar Borůvka). Galbūt šio mokslininko darbas buvo nepastebėtas todėl, kad straipsnį jis išspausdino čekų kalba. Dar daugiau – pasirodo, Primo algoritmas taip pat buvo atrastas anksčiau kito čekų matematiko Vojtecho Jarniko (Vojtĕch Jarník), o algoritmui jau buvo prigijęs Primo algoritmo vardas.
Šiame skyrelyje aprašysime visus tris algoritmus MJM paieškai, tačiau pateiksime tik Primo algoritmo realizaciją. Tam yra rimta priežastis – Primo algoritmo MJM paieškai realizacija skiriasi nuo Dijkstros trumpiausio kelio algoritmo vos keliomis eilutėmis.
Visi trys algoritmai remiasi godžiąja strategija, t.y. kiekviename
žingsnyje pasirenkamas palankiausias tuo momentu sprendimas. Ko gero,
aiškiausias yra Kruskalo algoritmas, kuriuo konstruojamas MJM
prijungiant grafo briaunas. Iš pradžių medis yra tuščias, o
kiekvienu tolesniu žingsniu prijungiama pigiausia (mažiausio svorio)
briauna, kurios prijungimas nesudarytų ciklo. Medis baigiamas
konstruoti, kai daugiau negalima prijungti nė vienos briaunos. Kadangi
medis turi lygiai 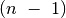 briauną, tai MJM sudaryti prireikia
lygiai
briauną, tai MJM sudaryti prireikia
lygiai 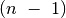 žingsnių (
žingsnių (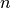 – grafo viršūnių
skaičius).
– grafo viršūnių
skaičius).
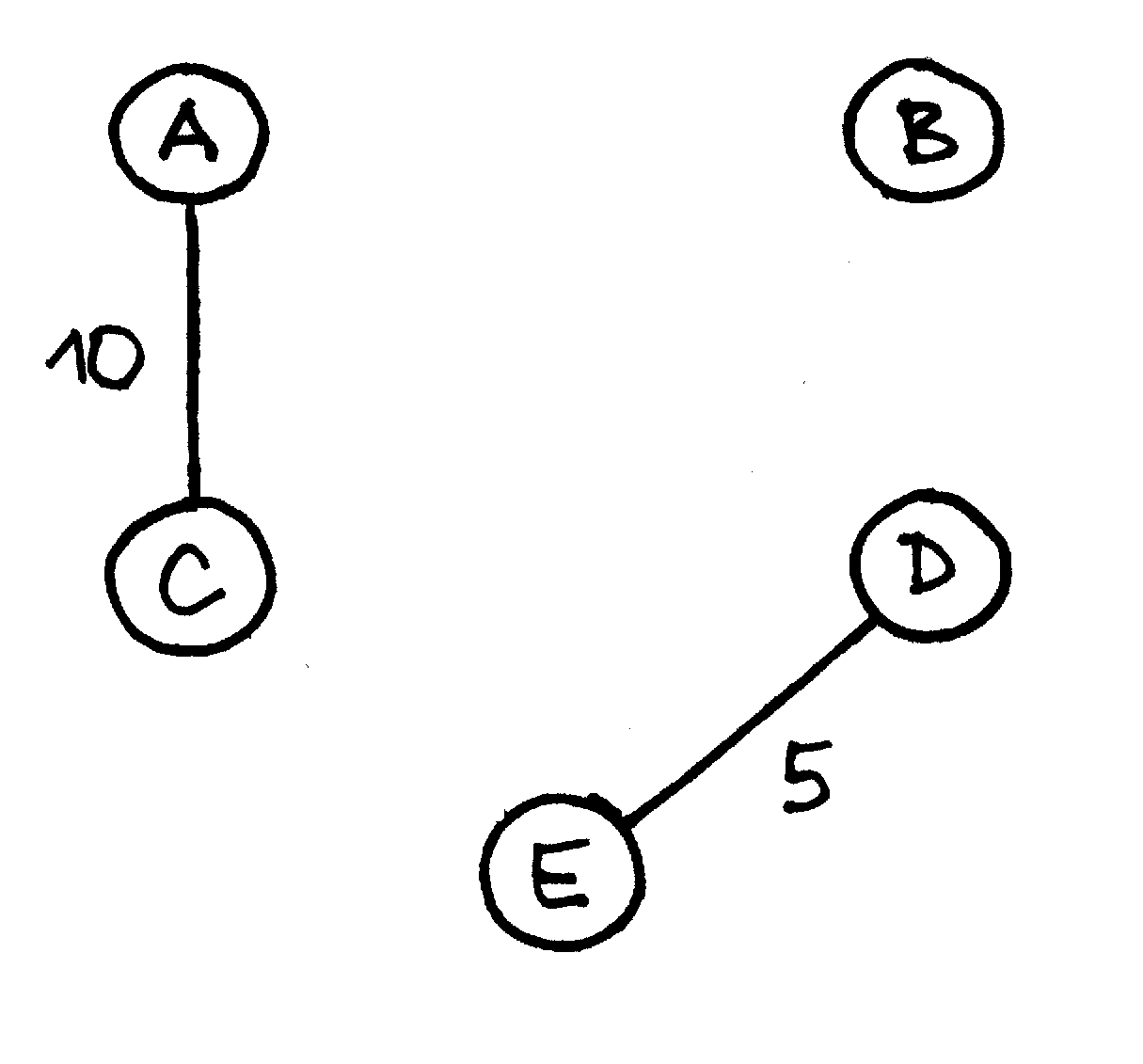
Randama pigiausia briauna (jos kaina – 5) ir įtraukiama į MJM |
|
Pasirenkama kita pigiausia briauna (yra dvi tokios
briaunos |
|
Kita pigiausia briauną yra |
|
Tolesnė pigiausia briauna yra |
|
Prijungiama ketvirtoji pigiausia briauna
( |
Nors Kruskalo algoritmą suprasti labai lengva, jį realizuoti sudėtingiau, nes nuolat tenka tikrinti, ar prijungiant briauną nesusidarys ciklas.
Primo algoritmu taip pat MJM konstruojamas prijungiant grafo briaunas, tačiau pradedama nuo medžio, kurį sudaro viena laisvai pasirinkta viršūnė. Prijungiamoji briauna taip pat turi būti pigiausia, tačiau tenkinti kitokią sąlygą negu Kruskalo algoritme: lygiai viena briaunos viršūnė turi priklausyti konstruojamam medžiui. Ši sąlyga garantuoja, kad prijungiant briauną nesusidarys ciklas.
Toliau iliustruojama, kaip veikia Primo algoritmas. Prijungtos viršūnės spalvinamos pilkai, ir iliustracijose pateikiamos tik tos briaunos, kurios yra arba jau prijungtos prie MJM, arba kurių lygiai viena viršūnė priklauso MJM.
Pasirenkame pradinę viršūnę (pavyzdžiui,
|
|
Prie sudarinėjamo MJM, kuris kol kas turi dvi
viršūnes |
|
Toliau pigiausiai galima prijungti viršūnę
|
|
Liko viena neprijungta viršūnė; ją pigiausiai
galima prijungti briauna |
Kaip jau minėjome, Primo algoritmo realizacija labai primena Dijkstros algoritmą. Pradedant nuo tuščio medžio, kiekvienu žingsniu išsirenkama ir prijungiama nauja viršūnė. Todėl, kaip ir Dijkstros algoritme, visos viršūnės paskirstomos į dvi aibes: prijungtų prie konstruojamo medžio ir dar neprijungtų. Kiekvienu žingsniu norėsime prie medžio prijungti tą viršūnę, kurią galima prijungti pigiausia briauna. Todėl Primo algoritmas išlaiko mažiausią žinomą kiekvienos viršūnės prijungimo kainą. Pradžioje šios kainos nustatomos begalinės visoms viršūnėms, išskyrus pasirinktąją. Kiekvienu žingsniu prijungus viršūnę su mažiausia prijungimo kaina, galbūt bus rastas geresnis būdas, kaip prie medžio prijungti jos kaimynes. Todėl peržiūrimos ir, jei reikia, atnaujinamos prijungtosios viršūnės kaimynių prijungimo kainos. Atliekamų žingsnių skaičius lygus grafo viršūnių skaičiui.
Toliau pateiktame algoritme grafas vaizduojamas kaimynystės matrica, o minimalus jungiamasis medis – pirminumo masyvu.
const BEGALINIS = MAXINT;
MAXN = ...; { maksimalus viršūnių skaičius }
type grafas = record
n : longint; { viršūnių skaičius }
svoris : array [1..MAXN,
1..MAXN] of integer;
end;
masyvas = array [1..MAXN] of integer;
logmas = array [1..MAXN] of boolean;
procedure Primo(var G : grafas;
var pirminė : masyvas);
{ ieškomasis medis grąžinamas masyve „pirminė“ }
var prijungta : logmas;
kaina : masyvas;
v, u, min : integer;
begin
{ įrašomos pradinės masyvų reikšmės }
for u := 1 to G.n do begin
kaina[u] := BEGALINIS;
pirminė[u] := -1;
prijungta[u] := false;
end;
v := 1;
kaina[v] := 0; { pradėsime nuo pirmos viršūnės }
while v <> 0 do begin
{ jei v <> 0, tai rasta viršūnė, kurią galima prijungti }
prijungta[v] := true;
for u := 1 to G.n do { nagrinėjamos kaimynės }
if (not prijungta[u]) and
(G.svoris[v, u] < BEGALINIS) and
(kaina[u] > G.svoris[v, u])
then begin { viršūnę u verčiau jungti prie v }
kaina[u] := G.svoris[v, u];
pirminė[u] := v;
end;
{ randama tolesnė kandidatė -
dar neprijungta viršūnė su mažiausia prijungimo kaina }
v := 0;
min := BEGALINIS;
for u := 1 to G.n do
if (not prijungta[u]) and (kaina[u] < min)
then begin
v := u;
min := kaina[u];
end;
{ jei jokia viršūnė nerasta, tai v = 0 ir ciklas nutraukiamas }
end;
end;
/*
Pastaba: pirmiau pateikiamas Primo algoritmo kodas, analogiškas kodui, užrašytam Paskalio kalba,
o žemiau - efektyvus, naudojantis duomenų struktūrą priority_queue (kaip ir efektyvioje
Dijkstros algoritmo realizacijoje).
Taip pat verta paminėti, kad olimpiadose patogiausia naudoti Kruskalio algoritmą MJM rasti,
kurio realizacijoje naudojama duomenų struktūra "nesikertančių aibių sąjunga" (trumpinama, DSU).
Apie Kruskalio algoritmą galite pasiskaityti čia: https://cp-algorithms.com/graph/mst_kruskal_with_dsu.html
*/
const int BEGALINIS = ...; // kažkoks pakankamai didelis skaičius, pavyzdžiui 1e9
const int MAXN = ...; // maksimalus viršūnių skaičius
int n; // viršūnių skaičius
int svoris[MAXN][MAXN];
int pirmine[MAXN];
vector<int> antrSar[MAXN]; // antrinių viršūnių sąrašas
bool prijungta[MAXN];
int kaina[MAXN];
void primo () {
// ieškomas medis grąžinamas masyve "pirmine"
// įrašomos pradinės masyvų reikšmės
for (int u = 0; u < n; u++) {
kaina[u] = BEGALINIS;
pirmine[u] = -1;
prijungta[u] = false;
}
int v = 0;
kaina[v] = 0; // pradėsime nuo viršūnės su numeriu 0
while (v != -1) {
// jei v != -1, tai rasta viršūnė, kurią galima prijungti
prijungta[v] = true;
for (int u = 0; u < n; u++) { // nagrinėjamos kaimynės
if (!prijungta[u] && svoris[v][u] < BEGALINIS && kaina[u] > svoris[v][u]) {
// viršūnę u verčiau prijungti prie v
kaina[u] = svoris[v][u];
pirmine[u] = v;
}
}
// randama tolesnė kandidatė - dar neprijungta viršūnė su mažiausia prijungimo kaina
v = -1;
int minKaina = BEGALINIS;
for (int u = 0; u < n; u++) {
if (!prijungta[u] && kaina[u] < minKaina) {
v = u;
minKaina = kaina[u];
}
}
// jei jokia viršūnė nerasta, tai v = -1 ir ciklas nutraukiamas
}
}
// Primo algoritmo realizacija, naudojanti priority_queue
vector<pair<int, int>> adj[MAXN];
/*
adj[i] yra i-tosios viršūnės kaimynų sąrašas, kur
adj[i][j].first yra j-tosios kaimynės numeris
adj[i][j].second yra briaunos, jungiančios i-tąją viršūnę su jos j-tąja kaimyne, svoris
*/
void primo () {
// įrašomos pradinės masyvų reikšmės
for (int u = 0; u < n; u++) {
kaina[u] = BEGALINIS;
pirmine[u] = -1;
prijungta[u] = false;
}
kaina[0] = 0;
priority_queue<pair<int, int>, vector<pair<int,int>>, greater<pair<int,int>>> q; // priority_queue, kurios top() elementas visad yra mažiausias
q.push({kaina[p], p}); // į q visados dedam poras {kaina[i], i}, nes tada q.top() elementas visad būs mažiausios kainos
while (!q.empty()) {
int v = q.top().second;
if (!prijungta[v]) {
prijungta[v] = true;
for (auto p : adj[v]) { // einame per viršūnės v kaimynus
int u = p.first; // kaimynės numeris
int w = p.second; // briaunos tarp v ir u svoris
if (kaina[u] > w) {
// verčiau į u eiti per v
kaina[u] = w;
pirmine[u] = v;
q.push ({kaina[u], u});
}
}
}
}
}
Įvykdžius algoritmą, minimaliam jungiamajam medžiui priklauso
briaunos (v, pirminė[v]), kur  – bet kuri grafo
viršūnė, išskyrus pradinę. Primo algoritmo sudėtingumas –
– bet kuri grafo
viršūnė, išskyrus pradinę. Primo algoritmo sudėtingumas –
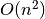 .
.
Aprašysime ir nepelnytai pamirštą, tačiau ne mažiau elegantišką nei Primo ar Kruskalo algoritmai, Boruvkos algoritmą.
Algoritmas operuoja medžių sąrašu. Pradžioje šį sąrašą sudaro
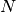 medžių, kurių kiekvieną sudaro viena (kiekvienam kita)
grafo viršūnė. Tuomet paeiliui nagrinėjami visi medžiai. Kiekvienam
jų randama pigiausia į medį ateinanti, tačiau medžiui
nepriklausanti briauna, ir įtraukiama į jį. Jei keliems medžiams
buvo parinkta ta pati pigiausia briauna, tai tie medžiai sujungiami.
Veiksmai kartojami tol, kol lieka tik vienas medis. Tai ir bus minimalus
jungiamasis medis.
medžių, kurių kiekvieną sudaro viena (kiekvienam kita)
grafo viršūnė. Tuomet paeiliui nagrinėjami visi medžiai. Kiekvienam
jų randama pigiausia į medį ateinanti, tačiau medžiui
nepriklausanti briauna, ir įtraukiama į jį. Jei keliems medžiams
buvo parinkta ta pati pigiausia briauna, tai tie medžiai sujungiami.
Veiksmai kartojami tol, kol lieka tik vienas medis. Tai ir bus minimalus
jungiamasis medis.
Uždavinys Tinklas 1¶
Firma ALFA gavo užsakymą: sujungti
kompiuterių ir
komutatorių 2 į vieną laidinį tinklą. Reikalavimai tinklo architektūrai tokie:
Kiekvienas kompiuteris tiesiogiai vienu laidu sujungiamas su bet kuriuo vienu (ir tik vienu) komutatoriumi;
Prie kiekvieno komutatoriaus tiesiogiai laidais galima prijungti bet kokį skaičių kitų įrenginių (kompiuterių arba komutatorių); du įrenginiai tiesiogiai sujungiami vienu laidu;
Visi
komutatorių ir
kompiuterių turi sudaryti jungų tinklą, t. y. bet kuris įrenginys turi būti tiesiogiai arba netiesiogiai (per kitus įrenginius) sujungtas su visais kitais;
Užduotis. Duotos kompiuterių ir komutatorių sujungimo kainos. Reikia rasti tokią tinklo jungimų schemą, kurios kaina būtų mažiausia.
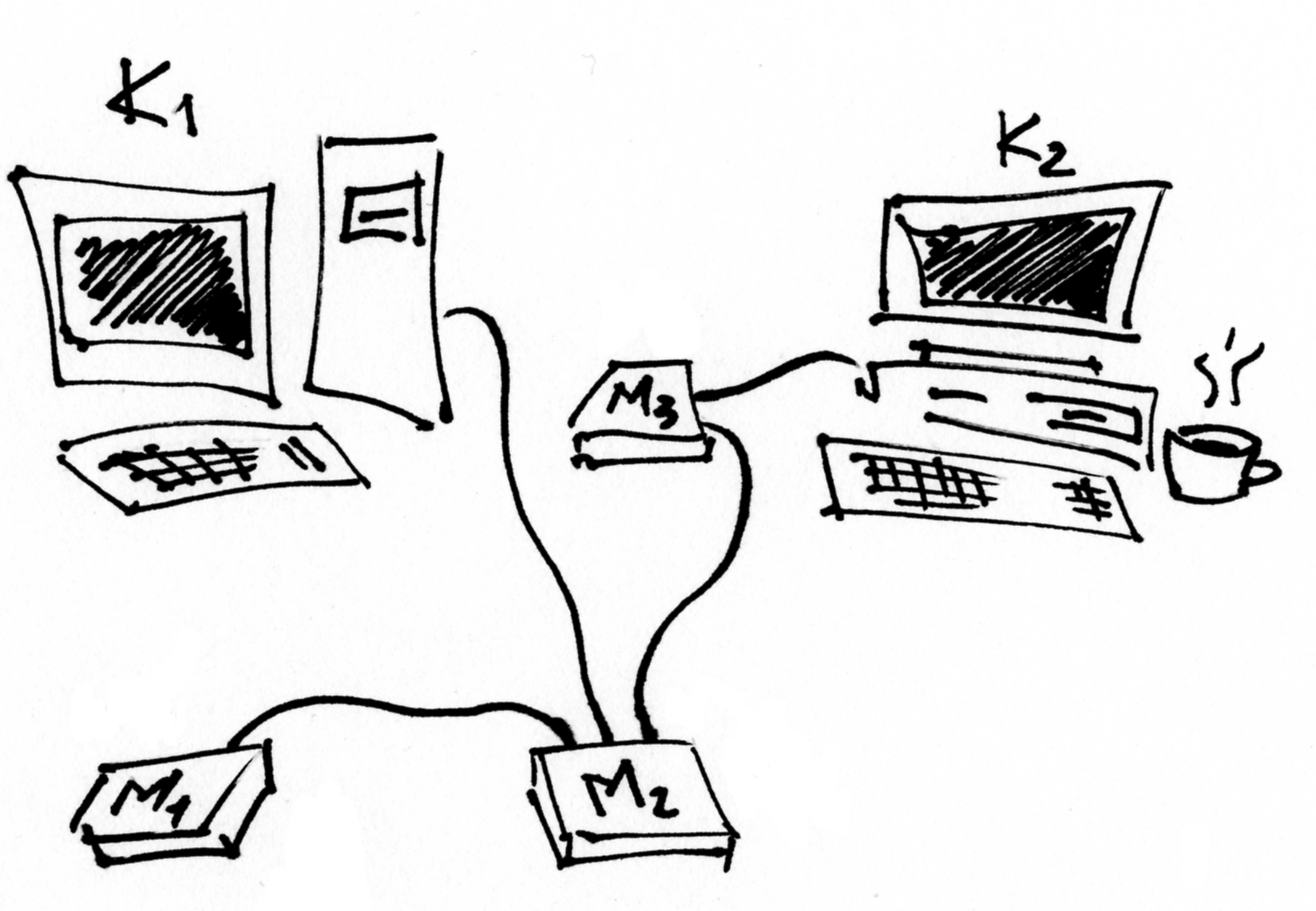
Fig. 70 Galima dviejų kompiuterių ir trijų komutatorių jungimo į tinklą schema¶
Kiekvienas kompiuteris turi būti prijungtas tik prie vieno įrenginio, būtent, komutatoriaus. Kadangi kompiuterį galime prijungti prie bet kurio iš jų, tai išsirinksime tą komutatorių, prie kurio prijungti kompiuterį yra pigiausia.
Tačiau visi įrenginiai turi sudaryti jungų tinklą, todėl komutatoriai turės būti sujungti tarpusavyje. Žinomos kiekvieno galimo jungimo kainos, todėl šiam jungimui rasti galime pritaikyti bet kurį minimalaus jungiamojo medžio paieškos algoritmą.
Pateiktame programos tekste visi įrenginiai sunumeruoti nuosekliai:
komutatoriai nuo 1 iki 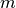 , o kompiuteriai – nuo
, o kompiuteriai – nuo
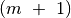 iki
iki 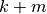 . Procedūrai perduodamas užpildytas
įrenginių jungimo kainų masyvas, taip pat įrenginių skaičius
(
. Procedūrai perduodamas užpildytas
įrenginių jungimo kainų masyvas, taip pat įrenginių skaičius
(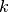 ir
ir 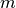 ). Grafas vaizduojamas briaunų svorių matrica
(žr. skyrelį Svoriniai grafai).
). Grafas vaizduojamas briaunų svorių matrica
(žr. skyrelį Svoriniai grafai).
const BEGALINIS = MAXINT;
MAXM = ...; { maksimalus komutatorių skaičius }
MAXK = ...; { maksimalus kompiuterių skaičius }
type masyvas = array [1..MAXM] of integer;
jungimas = record
įrenginysA, įrenginysB : integer;
end;
jungimų_mas =
array [1..MAXM + MAXK] of jungimas;
kainų_mas = array [1..MAXM + MAXK,
1..MAXM + MAXK] of integer;
procedure rask_jungimus(var kaina : kainų_mas;
m, k : integer;
var jung_sk,
jung_kaina : integer;
var jungimai : jungimų_mas);
{ k – kompiuterių, m – komutatorių skaičius, „kaina“ – įrenginių jungimo
kainų masyvas; atsakymas pateikiamas masyve „jungimai“ }
procedure junk(a, b : integer);
{ įrenginys a sujungiamas su įrenginiu b }
begin
jung_sk := jung_sk + 1;
jungimai[jung_sk].įrenginysA := a;
jungimai[jung_sk].įrenginysB := b;
jung_kaina := jung_kaina + kaina[a, b];
end;
var i, j, t : integer;
g : grafas;
pirminė : masyvas;
begin
jung_sk := 0; jung_kaina := 0;
{ prijungiame kiekvieną kompiuterį prie „artimiausio“
komutatoriaus (kompiuteriai sunumeruoti nuo (m + 1)
iki (m + k), komutatoriai - nuo 1 iki m) }
for i := m + 1 to m + k do begin
t := 1;
for j := 1 to m do
if kaina[i, t] > kaina[i, j] then t := j;
junk(i, t);
end;
{ komutatorių jungimui sudarome grafą ir randame
minimalų jungiamąjį medį }
g.n := m;
for i := 1 to m do
for j := 1 to m do
if i <> j then
g.svoris[i, j] := kaina[i, j]
else { jei i = j, tai briaunos (kilpos) nėra }
g.svoris[i, j] := BEGALINIS;
{ pagal Primo algoritmą randamas MJM }
Primo(g, pirminė);
{ medžio briaunos yra (i, pirminė[i]), visoms i, išskyrus 1 }
for i := 2 to g.n do
junk(i, pirminė[i]);
end;
const int BEGALINIS = ...; // kažkoks pakankamai didelis skaičius, pavyzdžiui 1e9
const int MAXM = ...; // maksimalus komutatorių skaičius
const int MAXK = ...; // maksimalus kompiuterių skaičius
int k; // kompiuterių skaičius
int m; // komutatorių skaičius
pair<int, int> jungimai[MAXM + MAXK]; // masyvas, kuriame bus pateikiamas atsakymas
int kaina[MAXM + MAXK][MAXM + MAXK]; // įrenginių jungimo kainų masyvas
int jungSk;
int jungKaina;
void junk (int a, int b) {
// įrenginys a sujungiamas su įrenginiu b
jungimai[jungSk].first = a;
jungimai[jungSk].second = b;
junkSk++;
jungKaina += kaina[a][b];
}
void raskJungimus () {
jungSk = 0;
jungKaina = 0;
/*
prijungiame kiekvieną kompiuterį prie "artimiausio" komutatoriaus
(kompiuteriai sunumeruoti nuo m iki m+k-1, komutatoriai - nuo 0 iki m-1
*/
for (int i = m; i < m+k; i++) {
int t = 0;
for (int j = 0; j < m; j++)
if (kaina[i][t] > kaina[j][t])
t = j;
junk(i, t);
}
// komutatorių jungimui sudarome grafą ir randame minimalų jungiamąjį medį
n = m;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
if (i != j)
svoris[i][j] = (i != j ? kaina[i][j] : BEGALINIS);
// pagal Primo algoritmą randamas MJM
Primo ();
// medžio briaunos yra (i, pirmine[i]), visoms i, išskyrus 0
for (int i = 1; i < n; i++)
junk (i, pirmine[i]);
}
Išnašos
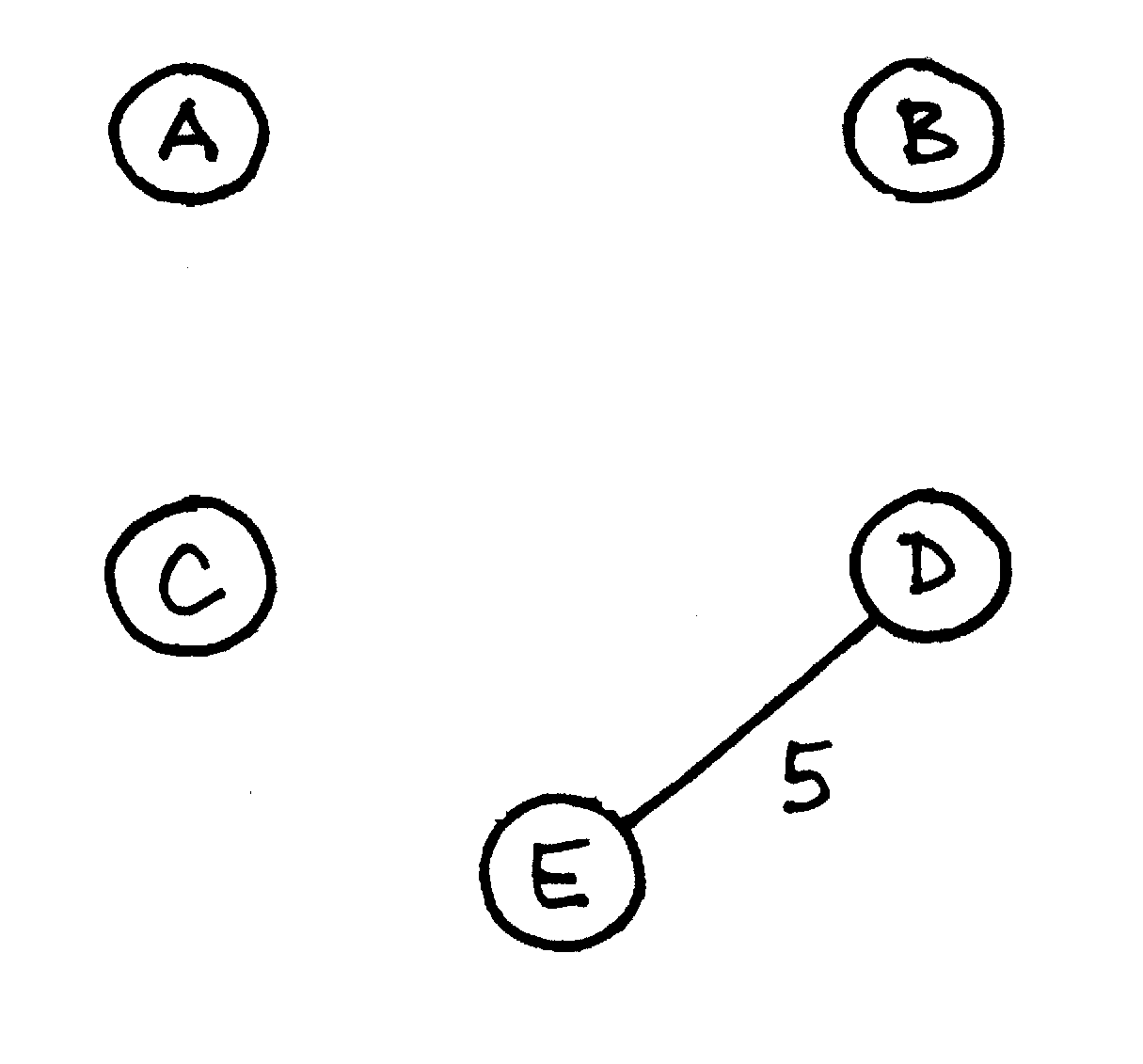
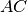 ir
ir 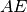 , imama bet kuri)
ir įtraukiama į MJM
, imama bet kuri)
ir įtraukiama į MJM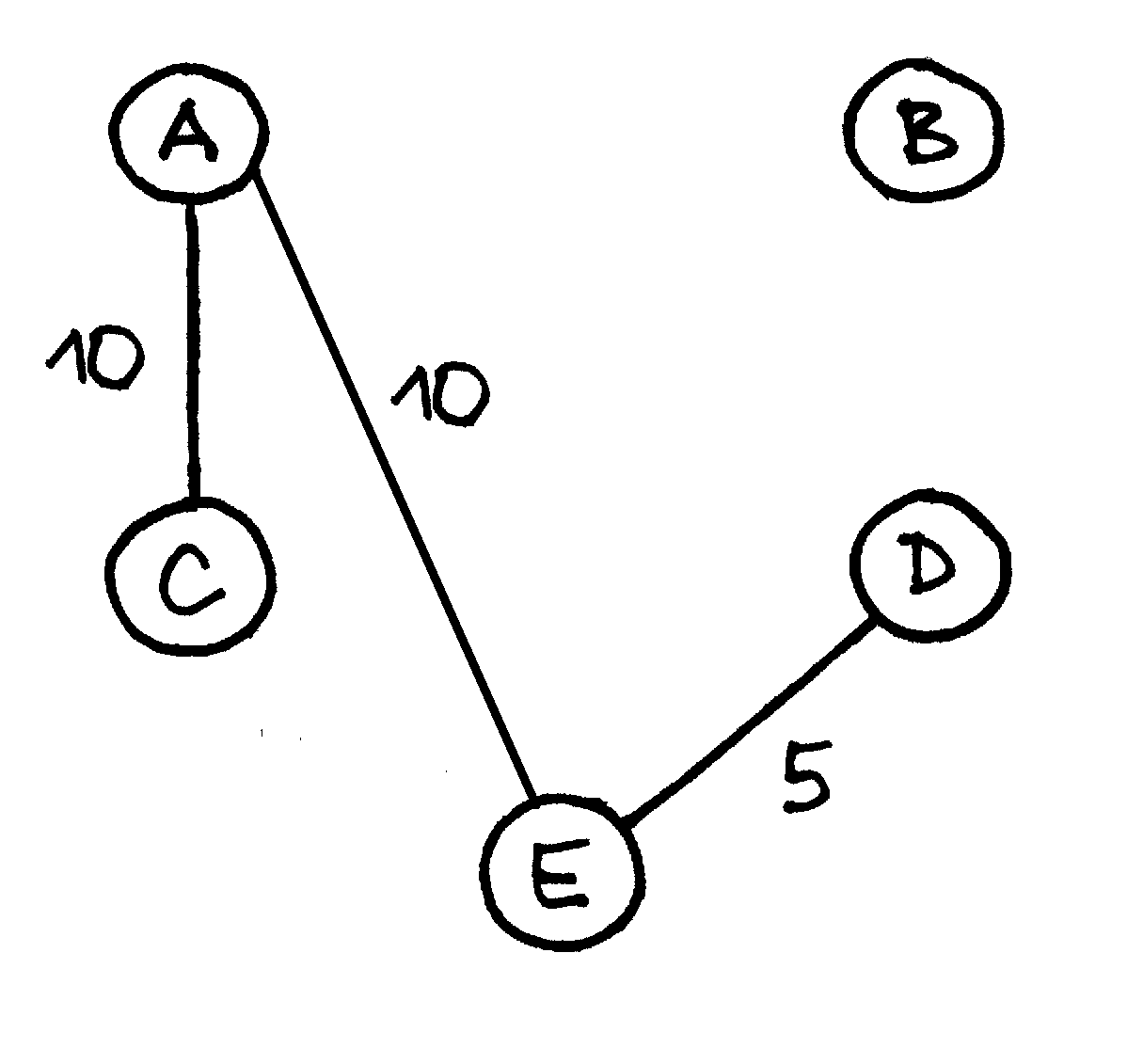
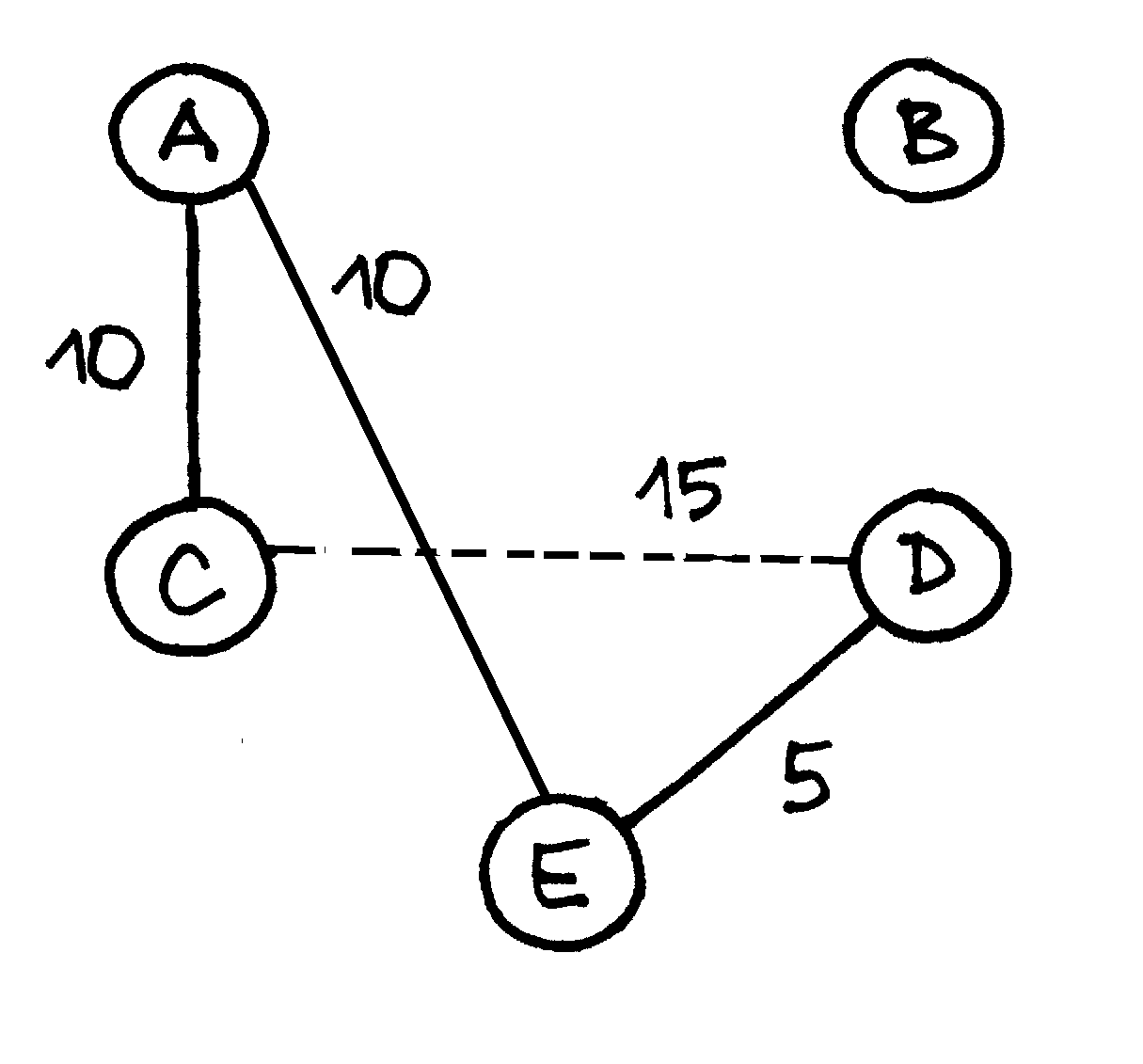
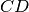 (jos
kaina 15), tačiau jos įtraukti į MJM negalima, nes
susidarytų ciklas, tad ši briauna praleidžiama
(jos
kaina 15), tačiau jos įtraukti į MJM negalima, nes
susidarytų ciklas, tad ši briauna praleidžiama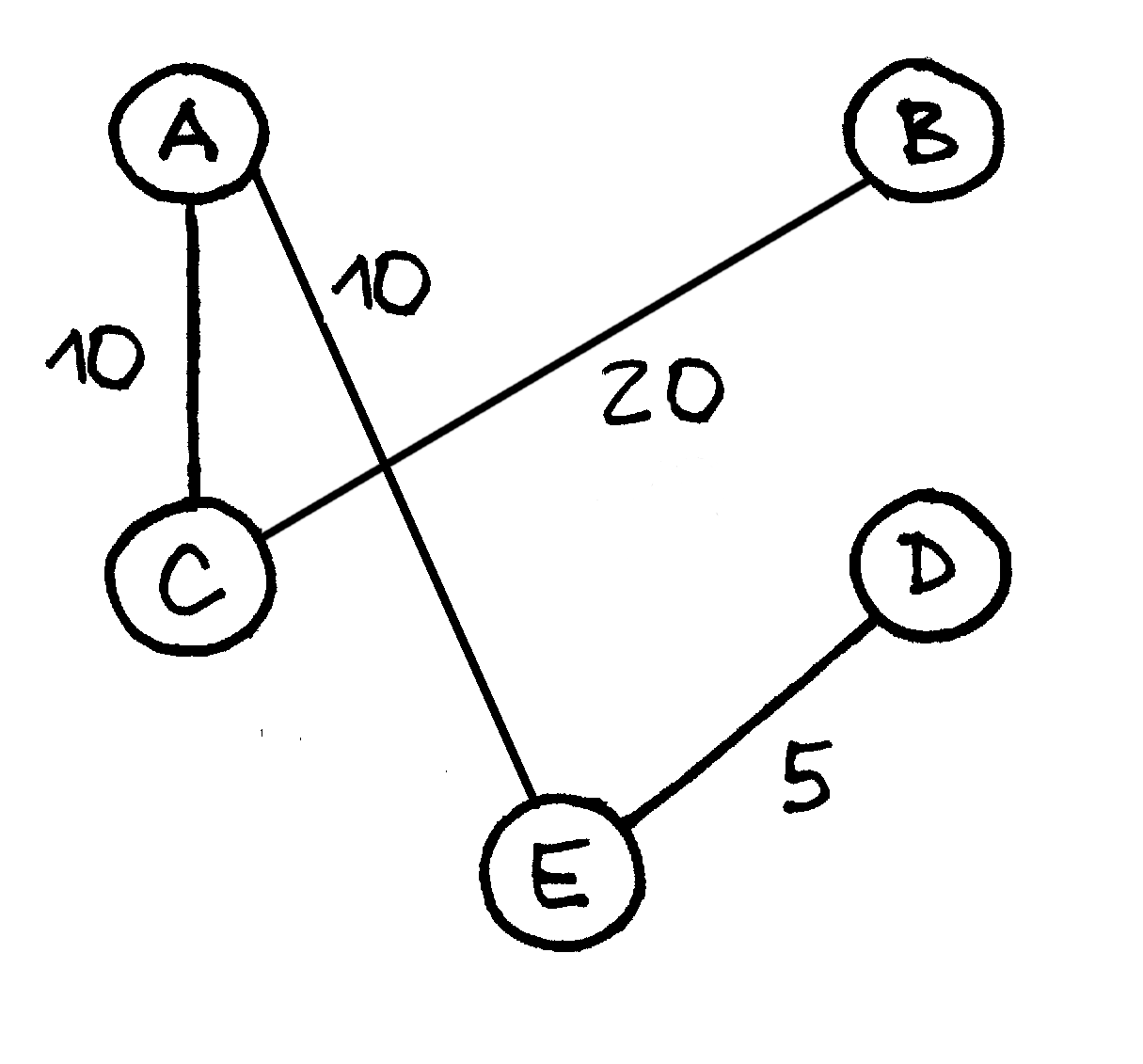
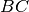 , jos kaina 20) ir gaunamas MJM; jo]
kaina – 45
, jos kaina 20) ir gaunamas MJM; jo]
kaina – 45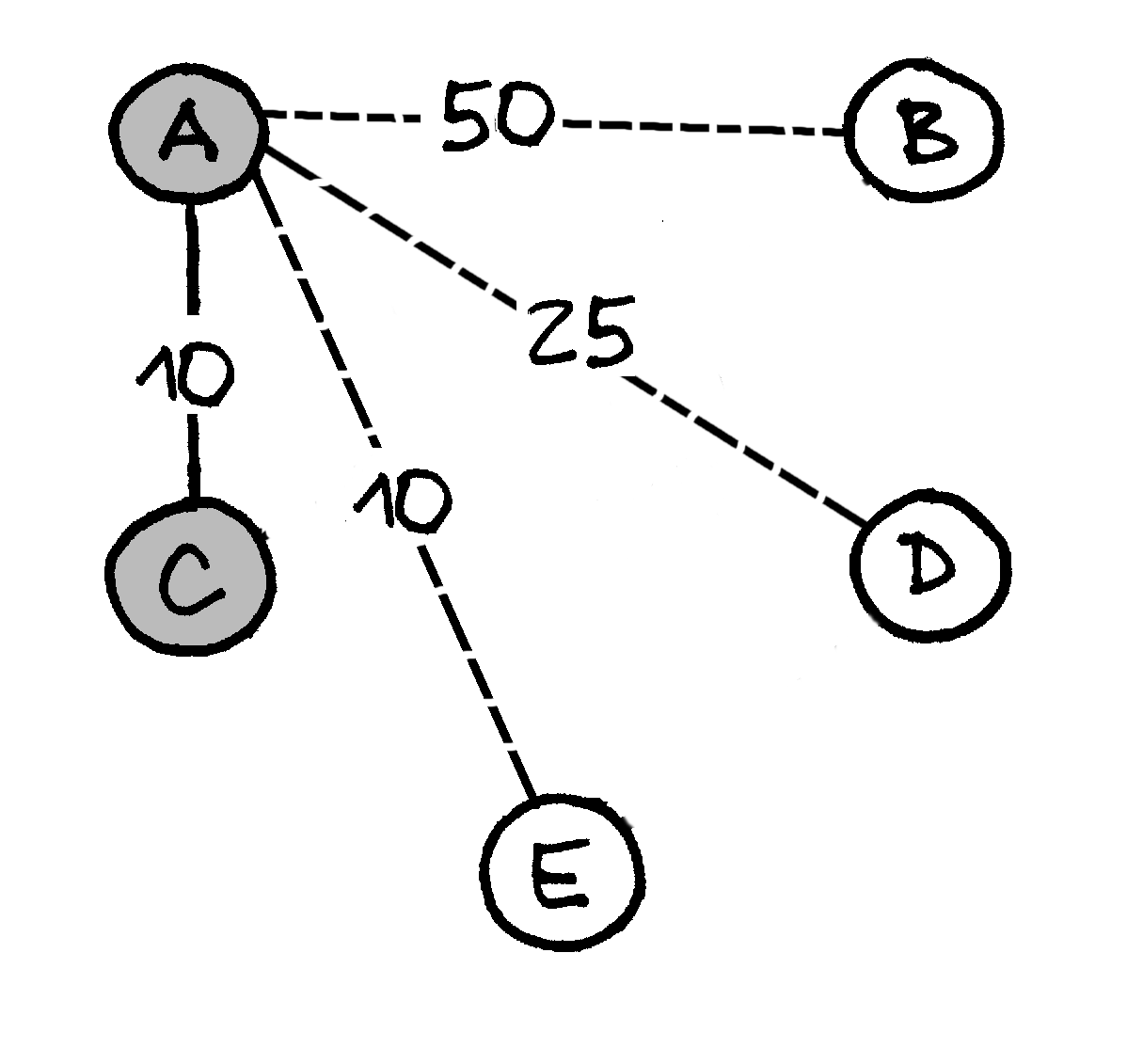
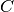 arba
arba 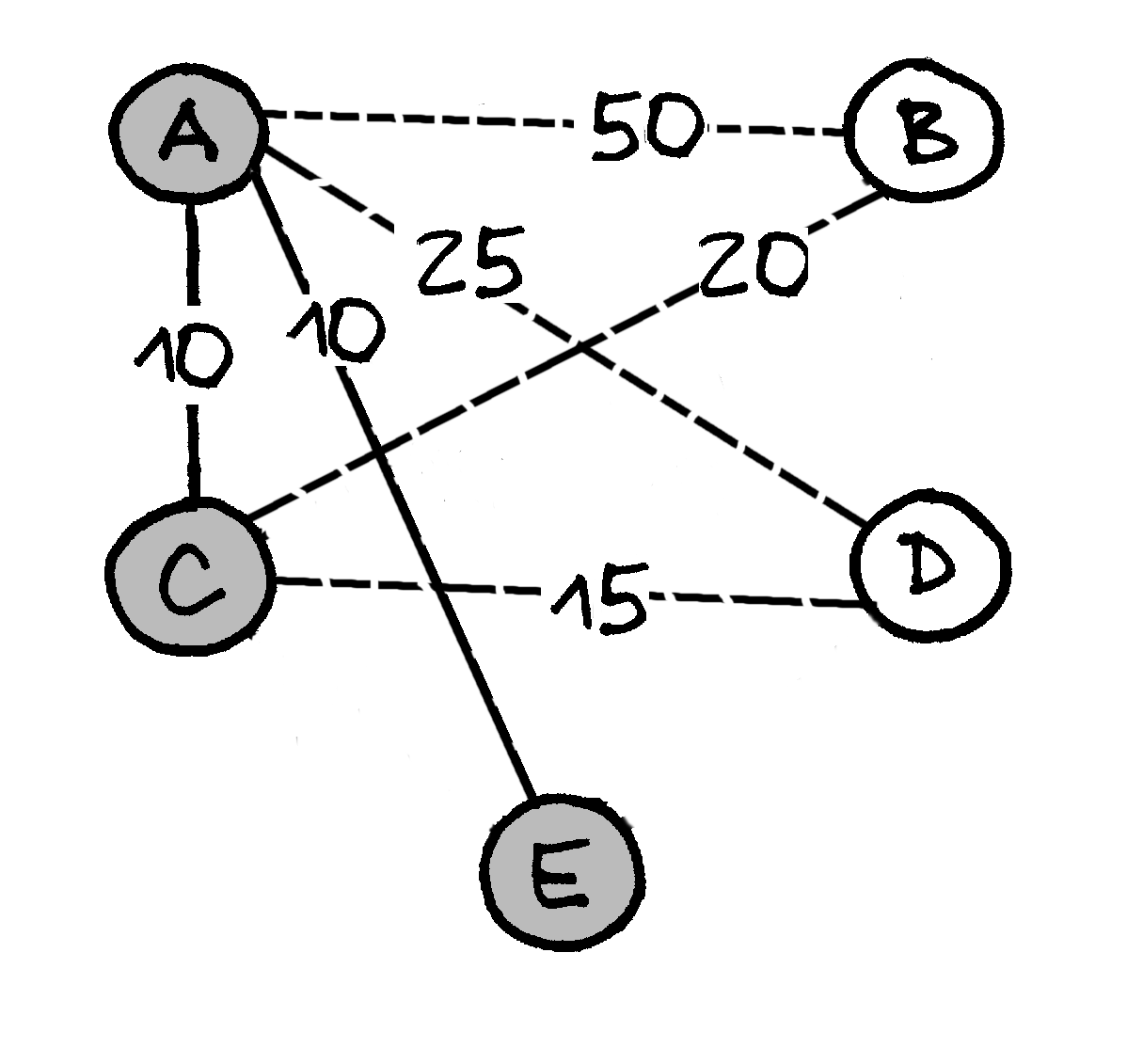
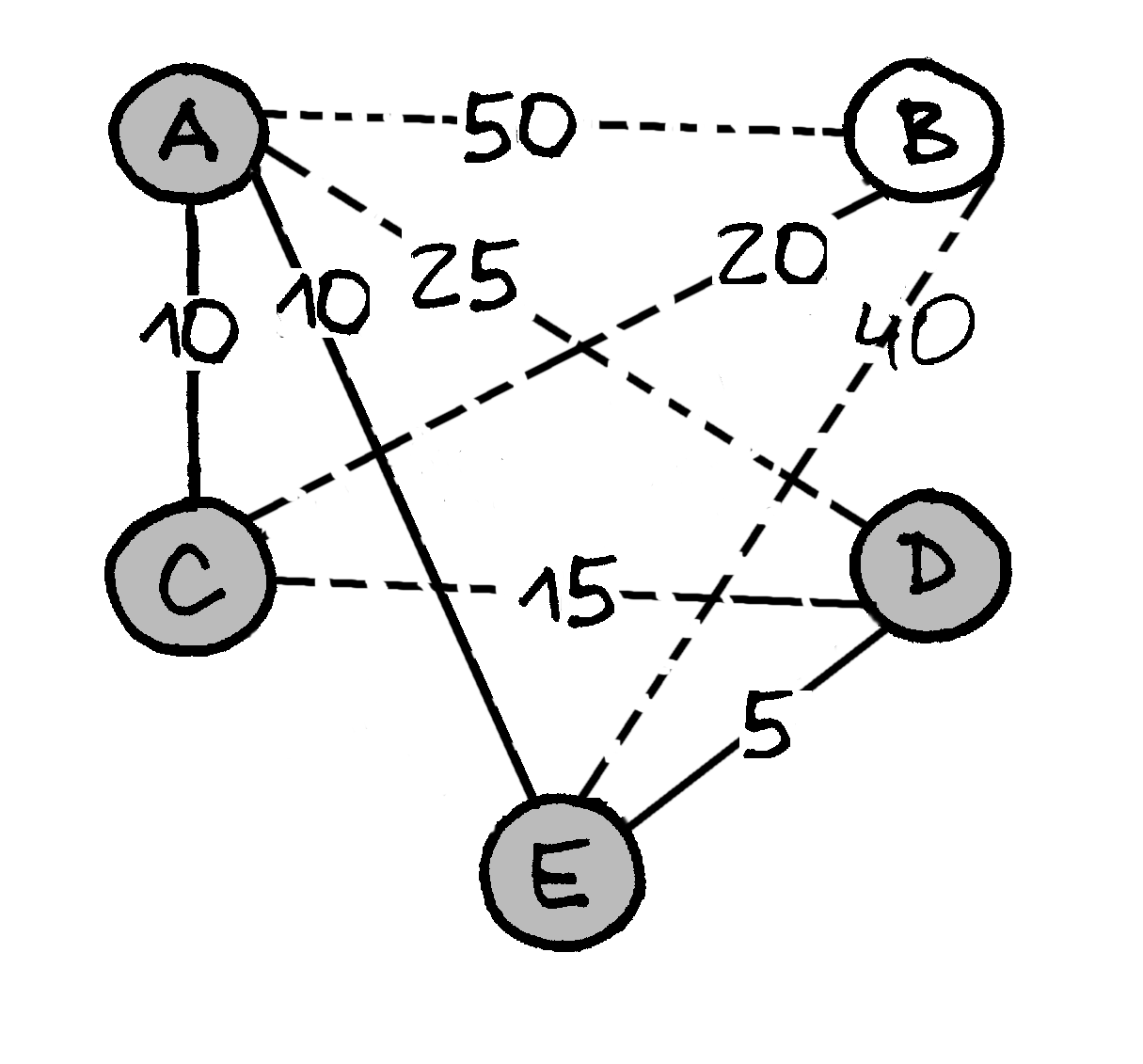
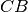 , jos svoris –
20; gauname
, jos svoris –
20; gauname